Квантовые системы

Интерференция электронов из различных источников

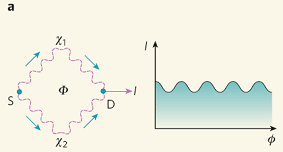
Тот факт, что электрон, будучи частицей, обладает еще и волновыми свойствами (корпускулярно-волновой дуализм), убедительно демонстрируют эксперименты по интерференции электронов при их прохождении через две параллельные друг другу щели в пластинке. Наблюдается и интерференция электронов в металлических проводниках [1]: если разделить электронный пучок от одного источника S на две части, а затем опять свести их воедино, то при наличии магнитного поля фазы "электронных волн" (строго говоря – квантовых амплитуд вероятности), распространяющихся разными путями, изменятся по-разному. В зависимости от разности набежавших фаз (определяемых величиной потока магнитного поля F через площадь контура, образованного траекториями электронов при их движении от источника к стоку), эти волны могут интерферировать как "конструктивно", так и "деструктивно". Поэтому сила тока I после воссоединения двух "половинок" пучка является периодической функцией F (см. рис.1а).

 

Рис.1. a Схематическое изображение "одноэлектронного интерферометра". S – источник, D – сток. F – поток магнитного поля через площадь контура, образованного двумя различными путями электронов от источника к стоку. χ1 и χ2 – изменения фазы электронной волновой функции на этих путях (χ1-χ2 ~ F). I – сила тока в контакте D.

А будут ли интерферировать электроны от двух различных источников? Ведь если каждому электрону отвечает своя "волна материи", не зависящая от волн других электронов, то интерференционной картинки можно и не получить.  Теория утверждает, что интерференция должна иметь место и в этом случае: согласно фундаментальному постулату квантовой механики, все электроны во Вселенной (как и любые элементарные частицы одного сорта) полностью идентичны и описываются одной и той же "волной материи", как бы связывающей их невидимой нитью. Но теория теорией, а наблюдать интерференцию электронов от разных источников на эксперименте долгое время не удавалось из-за технических сложностей. Первой здесь преуспела команда из Израиля (Weizmann Institute of Science) и Южной Кореи (Pusan National University), которая изготовила "двухэлектронный интерферометр" на основе двумерного электронного газа в гетероструктуре GaAs/AlGaAs [2]. За основу была взята идея, предложенная недавно в работе [3]: электронные пучки от двух источников S1 и S2 расщепляются на две части (каждый) так, что любая из четырех чаcтей может достичь одного из двух стоков D1 и D2, но при этом две "половинки" одного пучка соединяются не друг с другом, а только с "половинками" другого пучка. Средние величины силы тока <I1> и <I2> в контактах D1 и D2 равны нулю, так как фазы "электронных волн" в источниках S1 и S2 не коррелированы. А вот коррелятор <I1I2>, в который случайные фазы входят с противоположным знаком, оказывается периодической функцией потока F (см. рис.1b) – в полном соответствии с теорией.

 

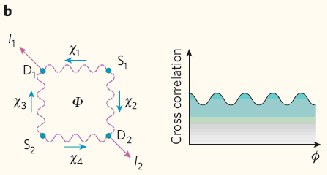
Рис.1 b. Схематическое изображение "двухэлектронного интерферометра". S1 и S2 – источники, D1 и D2 – стоки, F – поток магнитного поля. χ1, χ2, χ3 и χ4 – изменения фазы на различных путях. По вертикальной оси отложен коррелятор <I1I2>-<I1><I2> силы тока через контакты D1 и D2.

 

Таким образом (в который уже раз!) подтверждена справедливость квантового описания Природы. Интересно, что наблюдавшаяся в [3] "двухчастичная интерференция" имеет место для электронов, которые до этого никогда друг с другом не взаимодействовали. Эффекты такого рода уже предложено использовать для когерентного контроля многочастичных квантовых состояний [4].

  1. R.A. Webb et al., Phys. Rev. Lett. 54, 2696 (1985).

  2. I. Neder et al., Nature 448, 333 (2007).

  3. P. Samuelsson et al., Phys. Rev. Lett. 92, 026805 (2004).

  4. M. Kindermann, Nature 448, 262 (2007).

СВЕРХПРОВОДНИКИ

Расходимость верхнего критического поля в ферромагнитном
сверхпроводнике URhGe вблизи квантовой критической точки

В последние годы большое внимание уделяется исследованиям твердотельных систем вблизи квантовых критических точек (ККТ), разделяющих различные фазы при T=0. В окрестности ККТ могут возникать новые упорядоченные квантовые состояния, в том числе экзотические формы сверхпроводимости. В работе [1] коллектив физиков из Франции и Великобритании сообщил о наблюдении резкого роста Hc2 ферромагнитного сверхпроводника URhGe в окрестности ККТ, расположенной между фазами с различной ориентацией намагниченности (см. рис.1).

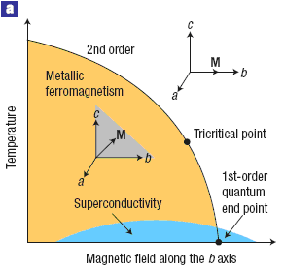Рис.1. Схематическое изображение фазовой диаграммы URhGe в координатах температура – компонента магнитного поля вдоль оси b. Сплошная линия разделяет спин-поляризованные состояния с различным направлением намагниченности M. Выше трикритической точки фазовый переход между этими состояниями является переходом второго рода, а ниже – переходом первого рода. При T = 0 эти состояния разделены квантовой критической точкой, в окрестности которой наблюдается "необычная" сверхпроводимость с Tc < 1 К и аномально большим для такой низкой Tc верхним критическим полем.

В узком диапазоне значений проекции магнитного поля на ось b (Hb) вблизи Hbc = 12 Тл обнаружена сверхпроводимость, сохраняющаяся вплоть до очень большой величины (Ha) проекции магнитного поля на ось a (см. рис.2).

 

 

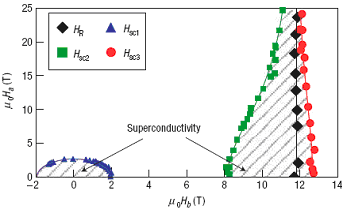
Рис.2. Критические величины Hsc1, Hsc2, Hsc3 компоненты магнитного поля вдоль оси a как функции компоненты Hb при
T = 0.5 К. HR – поле, при котором происходит переход между двумя различными ферромагнитными состояниями (см. рис.1). Области сверхпроводящей фазы заштрихованы.

 

При Hb ® Hbc критическая величина Ha возрастает без признаков насыщения (максимальная величина Ha в [1] составила 28 Тл, и это при том, что в родственном сверхпроводнике UGe2 с близкой Tc верхнее критическое поле всего лишь ~ 1 Тл). Принято считать [2], что куперовские пары в URhGe образованы электронами с одинаковой проекцией спина (триплетное спаривание) и имеют p-волновую орбитальную симметрию. В вопросе о механизме спаривания ясности пока нет. Полученные в [2] результаты могут подсказать теоретикам правильный путь.

Л.Опенов

  1. F.Levy et al., Nature Physics 3, 460 (2007).

  2. G.G.Lonzarich, Nature Physics 3, 453 (2007).

Какая поверхность Ферми в ВТСП?

В 1926 году итальянский физик Энрико Ферми предположил, что при низких температурах свободные электроны в металлах занимают только состояния с энергиями ε меньшими некоторой максимальной величины (именуемой c той поры энергией Ферми εF), а в состояниях с ε >εF электронов нет. Это предположение оказалось верным. В k-пространстве занятые электронами состояния отделены от свободных поверхностью, определяемой из условия ε(k)=εF и называемой поверхностью Ферми (ПФ). В простых металлах ее форма и размер зависят только от концентрации электронов и типа кристаллической структуры. ПФ большинства известных металлов были определены экспериментально и рассчитаны теоретически в 60-х годах прошлого века. После открытия в 1986 году высокотемпературных сверхпроводников много внимания уделялось исследованию их ПФ (в ВТСП поверхностью Ферми обычно называют ее проекцию на параллельную слоям CuO2 плоскость a-b, то есть фактически – контур Ферми). Но если в передопированных ВТСП с концентрацией дырок p ≈ 0.25 вид ПФ надежно установлен [1,2] (см. рис.) и согласуется с теоретическими расчетами, то в отношении недодопированных ВТСП (p » 0.1) ясности пока нет. Более того, данные фотоэмиссионной спектроскопии с угловым разрешением (ARPES) свидетельствуют о том, что при уменьшении концентрации носителей "большая" ПФ передопированных образцов не просто уменьшается в размере, а разбивается на несвязанные друг с другом участки – "фермиевские дуги" (Fermi arcs), то есть перестает существовать как собственно связная поверхность [3,4] (см. рис.). Считается, что это есть следствие наличия в ВТСП анизотропной псевдощели [4].

 

Поверхность Ферми в передопированных (красная линия) и недодопированных (синие линии) ВТСП. Зеленым цветом изображены "фермиевские дуги". Пунктирная линия соединяет точки (kx,ky) = (±π,0) и (0,±π) в двумерной зоне Бриллюена.

 

В работе [5] канадские и французские ученые представили результаты исследования ПФ недодопированных монокристаллов YBa2Cu3O6+y с
y = 0.5 (p » 0.1) и Tc = 57.5 К "классическим" способом – путем измерения осцилляций поперечного (холловского) электросопротивления Rxy как функции 1/H в параллельном оси c импульсном магнитном поле с H £ 62 Тл, достаточном для подавления сверхпроводимости. Выбор величины y = 0.5 не случаен. При этой величине атомы кислорода распределены по цепочкам Cu-O не хаотически, а образуют строго упорядоченную сверхструктуру (так называемая "фаза орто-II"), что в конечном итоге и позволило авторам [5] наблюдать четко выраженные квантовые осцилляции Rxy(1/H) при T = (1.5 ¸ 7.5) К > Tc(H). А результаты предыдущих измерений Rxy(H) неоднозначны из-за сильной дефектности недодопированных образцов. По частоте этих осцилляций и температурной зависимости их амплитуды в [5] была определена эффективная масса электрона m* = (1.9 ± 0.1) m0, где m0 – масса свободного электрона, и (самое главное) площадь "двумерной" ПФ в k-пространстве Ak = 5.1 нм-2. Эта величина Ak составляет всего лишь 1.9% от площади зоны Бриллюена и около 3% от площади "большой" ПФ в передопированном ВТСП Tl-2201, эффективный радиус которой kF ≈ 7 нм-1 [2]. В [5] обсуждаются две возможные причины такого резкого "сужения" ПФ:

1) специфика зонной структуры YBa2Cu3O6.5 (с учетом межэлектронного взаимодействия) и

2) резкая "перестройка" ПФ при понижении концентрации дырок p ниже некоторой критической величины pc, которую авторы [5] ассоциируют с критической точкой. В любом случае остается открытым вопрос о том, в какой именно области зоны Бриллюена расположена эта "маленькая" ПФ. Не исключено [5], что ПФ в YBa2Cu3O6.5 представляет собой четыре "кармана" (см. рис.), которые при исследовании фотоэмиссионных спектров [3,4] были приняты за "фермиевские дуги".

Л.Опенов

  1. N.E.Hussey et al., Nature 425, 814 (2003).             

  2. M.Plate et al., Phys.Rev.Lett. 95, 077001 (2005).

  3. M.R.Norman et al., Nature 392, 157 (1998).

  4. K.Shen et al., Science 307, 901 (2005). 

  5. N.Doiron-Leyraud et al., Nature 447, 565 (2007).

    6.

НАНОСТРУКТУРЫ, НАНОТЕХНОЛОГИИ, НАНОЭЛЕКТРОНИКА

Новый взгляд на переход металл-диэлектрик в двумерных системах

По характеру температурной зависимости удельного сопротивления R все вещества можно разделить на две основные категории: металлы и диэлектрики. При понижении температуры в типичных металлах R уменьшается (остаточное сопротивление при T=0 конечно), а в диэлектриках – неограниченно возрастает (см. рис.), так что в слабом электрическом поле ток через диэлектрик при T=0 не течет.

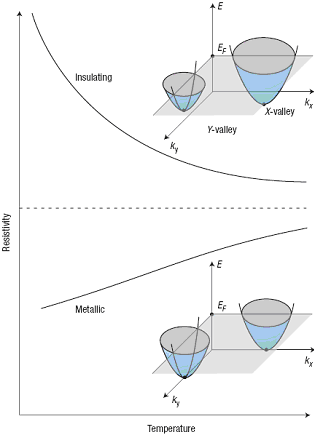
При одинаковой заселенности долин двумерная электронная система в AlAs является металлической, а при разной – диэлектрической.

Соответственно, принято говорить о металлическом и диэлектрическом типе проводимости. В классических (так называемых зонных) диэлектриках отсутствие тока при T=0 обусловлено отсутствием свободных носителей заряда (электронов в зоне проводимости и дырок в валентной зоне). Металл, в котором много свободных носителей, также можно перевести в диэлектрическое состояние. Для этого нужно увеличить концентрацию дефектов до определенной критической величины (зависящей от концентрации носителей), чтобы волновые функции электронов с энергией Ферми стали локализованными, и такие электроны не смогли участвовать в проводимости. Это касается обычных трехмерных металлов. По-другому обстоят дела в одномерных образцах: при любом сколь угодно слабом беспорядке все электронные состояния локализованы, и поэтому при T=0 реальный одномерный (точнее, квазиодномерный) образец будет диэлектриком независимо от концентрации электронов. Долгое время считалось [1], что при T=0 все двумерные системы тоже являются диэлектриками из-за квантового эффекта слабой локализации, обусловленной конструктивной интерференцией падающей на примесь и рассеянной в обратном направлении электронных волн.

Скейлинговая теория [1] была поставлена под сомнение после экспериментальной демонстрации смены диэлектрической зависимости R(T) на металлическую при увеличении концентрации носителей или ослаблении атомного беспорядка в двумерной электронной системе кремниевой МОП структуры [2]. Причина расхождения теории и эксперимента пока окончательно не выяснена. Многие сейчас склоняются к мнению, что ее нужно искать в электрон-электронном взаимодействии, которое первые теоретические модели вообще не учитывали. Об этом, в частности, свидетельствуют эксперименты [3] по поляризации электронных спинов в параллельном магнитном поле: даже если при H=0 двумерная система находится в металлической фазе, увеличение H приводит к переходу металл-диэлектрик. Согласно одной из точек зрения, переход в диэлектрическую фазу имеет место вследствие изменения эффективного взаимодействия между электронами из-за спинового разбаланса. Но конкретный характер этого изменения и микроскопический механизм его влияния на электрическую проводимость остаются непонятными.

В сложившейся ситуации чрезвычайно полезной может оказаться любая новая информация о переходе металл-диэлектрик в двумерии. В частности, большой интерес представляет изучение влияния других (помимо концентрации носителей, атомного беспорядка и спиновой поляризации) физических факторов на характер зависимости R(T). Сотрудники Princeton University (США) в качестве такого параметра использовали так называемую "поляризацию долин" – разницу между заселенностями двух подзон проводимости (X- и Y-долин) в квантовой яме AlAs толщиной около 10 нм [4]. В недеформированном слое AlAs эти долины вырождены и потому заполнены электронами в равной степени. Деформация образца вдоль оси X или Y приводит к нарушению кристаллической и, соответственно, электронной симметрии в плоскости XY, в результате чего вырождение долин снимается. Дно одной долины становится выше дна другой, и часть электронов (или даже все – в зависимости от величины деформации) "перетекает" из этой долины, понижая свою энергию (см. рис.). Полное число электронов при этом остается неизменным (в [4] их концентрация составила 2.5×1011 см-2, а подвижность – 3.6 м2/(В×с) при T = 0.3 К). Оказалось, что переход металл-диэлектрик имеет место лишь при сравнительно сильной поляризации и долин (относительная деформация e > 10-4), и спинов (H > 4 Тл). По мнению авторов [4], их результаты указывают на общую причину перехода, как при спиновом, так и при орбитальном разбалансе. Что же это за причина? Она может заключаться в изменении вовсе не межэлектронного взаимодействия, а степени экранирования хаотического потенциала заряженных примесей свободными носителями из-за перераспределения последних между разными одноэлектронными орбиталями [4,5]. Ослабление экранировки при поляризации спинов и долин эквивалентно усилению беспорядка, что и приводит к переходу в диэлектрическое состояние. Но прежде, чем делать окончательные выводы, необходимо попытаться провести эксперименты при как можно более низких температурах. Ведь пока все заключения делаются на основании анализа вида кривых R(T) при конечной температуре. И где гарантия, что металлическое (в нашем понимании) состояние двумерной системы не станет диэлектрическим при дальнейшем уменьшении температуры?
  1. E. Abrahams et al., Phys.Rev.Lett. 42, 673 (1979).
  2. S.V. Kravchenko et al., Phys.Rev.B 50, 8039 (1994).
  3. D. Simonian et al., Phys.Rev.Lett. 79, 2304 (1997).
  4. O. Gunawan et al., Nature Phys. 3, 388 (2007).
  5. J.H. Smet, Nature Phys. 3, 370 (2007).

ФУЛЛЕРЕНЫ И НАНОТРУБКИ

Упрочнение полимеров однослойными углеродными нанотрубками

Углеродные нанотрубки (УНТ), обладающие, как известно, рекордными механическими характеристиками, рассматриваются многими авторами как эффективное средство повышения прочностных свойств композитных полимерных материалов. Однако для реализации этой возможности необходимо добиться хорошего сопряжения между поверхностью УНТ и полимерной матрицей. Это обеспечивает эффективную передачу нагрузки от полимерного материала нанотрубке и, в конечном счете, приводит к повышению прочностных характеристик композита. В противном случае нанотрубка, помещенная внутрь полимерного материала, ведет себя там подобно «волосу в пироге» и не только не улучшает, но может даже ухудшить прочностные свойства полимера. Указанное сопряжение может быть реализовано в результате присоединения к поверхности УНТ радикалов, образующих химическую связь с молекулами полимера. Усилия, развиваемые во многих научных лабораториях мира и направленные на обеспечение сопряжения полимера с УНТ, начинают давать первые результаты. Так, недавно в одной из лабораторий Шанхая (Китай) [1] благодаря хорошему химическому сопряжению при содержании УНТ менее одной десятой процента было получено почти двукратное увеличение прочности ряда полимерных материалов. Коммерческие однослойные нанотрубки в течение 24 часов очищали обработкой концентрированной соляной кислотой. В качестве матрицы использовали такие полимеры, как полиаминофенилалкин (АРА), пленка полистирола (PS), а также сополимер стирола и полихлорметилстирола  (PS-co-PCMS). Образцы композита на основе АРА были приготовлены путем ультразвуковой обработки раствора олигомера в дихлорбензоле с добавлением некоторого количества нанотрубок с последующим введением изоамилнитрида и перемешиванием в течение 15 часов при температуре 60оС. Полученную суспензию растворяли в диметилфталате и после ультразвуковой обработки тщательно просушивали. Образцы на основе пленки полистирола готовили аналогичным образом с использованием раствора в тетрагидрофуране. При приготовлении образцов на основе сополимера (PS-co-PCMS) в качестве растворителя использовали толуол. Исследования, выполненные с помощью спектроскопии комбинационного рассеяния, а также Фурье-спектроскопии, показывают, что описанный способ получения композитов приводит к образованию прочной химической связи между полимерной матрицей и поверхностью УНТ. Это обусловлено присоединением химически активных радикалов к поверхности УНТ. Например, в случае матрицы полистирола таким радикалом является хлорбензол. Наличие такой связи приводит к заметному повышению прочностных характеристик композитов. Так, результаты проведенных испытаний указывают на увеличение прочности на разрыв пленки полистирола толщиной 70 мкм с 10,8 МПа до 19,7 МПа в результате добавления 0,06% однослойных УНТ. Аналогичным образом изменяются такие характеристики, как модуль упругости и предельное растяжение. Тем самым показано, что благодаря обеспечению хорошей передачи нагрузки от полимера к УНТ заметное упрочение полимерных композитов наблюдается уже при относительно небольших добавках нанотрубок.

А.В.Елецкий

  1. Long Xie et al. Macromolecules 40, 3296 (2007)

Углеродная нанотрубка как химический реактор

Наличие внутри углеродной нанотрубки (УНТ) полости, в которой может уместиться многоатомная молекула, позволяет рассматривать этот объект как сверхминиатюрный химический реактор, используемый для синтеза новых химических соединений. Преимущества такого подхода к химическому синтезу связаны с возможностью концентрации реагентов и катализатора в ограниченном объеме, а также с изоляцией реагентов от внешнего воздействия. Эффективность данного метода синтеза продемонстрирована недавно группой исследователей из Академии наук Китая [1], которым удалось осуществить внутри УНТ синтез этилового спирта. В качестве катализатора использовались наночастицы Rh and Mn с добавлением Li и Fe с поперечным размером 1-2 нм, которые (в результате использования капиллярных сил при ультразвуковой обработке и перемешивании) вводились (в весовом отношении 1:1:0.075:0.05) в полость многослойных УНТ, имеющих внутренний диаметр 4–8 нм и длину 250–500 нм. Наблюдения показывают, что около 80% наночастиц были распределены внутри каналов УНТ, в то время как остальная часть находилась на внешней поверхности нанотрубок. Для сравнения аналогичный катализатор был изготовлен с использованием в качестве основы SiO2. Сравнение показывает, что выход этанола при использовании реактора основе УНТ (84,4 моль моль-1Rh час-1) примерно вдвое превышает соответствующую величину для SiO2. При этом использование реактора на основе УНТ в течение 180 часов не привело к сколько-нибудь заметной дезактивации. Для установления характера влияния положения катализатора на скорость образования и выход этанола, было изготовлено два типа катализаторов, в одном из которых (RM-in-CNTs) смесь 5% Rh и 5% Mn помещали внутрь полости УНТ, в другом (RM-out-CNTs) – снаружи. Наблюдения показали, что свыше 75% частиц катализатора имели размеры 1–2 нм. Однако в процессе протекания химической реакции наблюдалась агрегация частиц, размер которых после 28 часов работы достигал 3–4 нм. Это сопровождалось снижением активности катализатора и скорости реакции, которая после 60 часов протекания реакции снизилась с 39 моль/час до 30 моль/час. После 112 часов работы размер частиц внутри нанотрубок увеличился до 4–5 нм, т.е. до размера внутреннего диаметра УНТ, в то время как частицы, расположенные снаружи УНТ, выросли до размера порядка 8 нм. Тем самым оказывается, что наличие стенок УНТ ограничивает агрегацию частиц катализатора и позволяет сохранить их активность в течение длительного времени.

А.В.Елецкий

      1. X.Pan et al. Nature Materials 6, 507 (2007).

Химический сенсор на основе углеродных нанотрубок

Высокая чувствительность электронных характеристик углеродных нанотрубок (УНТ) к наличию на их поверхности сорбированных молекул различного сорта позволяет рассматривать эти структуры как основу миниатюрного сенсора, способного определять состав и концентрацию различных примесей к атмосфере. В настоящее время ведутся интенсивные разработки конкретных устройств подобного рода, предназначенных для определения содержания ряда газов. Удачным примером таких разработок может служить работа сотрудников Сеульского университета (Ю.Корея) [1]. Авторы этой публикации сообщают о разработке сенсора, действие которого основано на пропускании исследуемого газа через внутреннюю полость УНТ. Многослойные УНТ длиной около 10 мкм с внешним диаметром 50±3 нм и средним расстоянием между трубками 110±1 нм были выращены методом химического осаждения паров (CVD) в результате пропускания смеси ацетилена с азотом в отношении 1:9 над мембраной из анодированного оксида алюминия в течение 2 минут при температуре 1000оС. Массив вертикально упорядоченных нанотрубок скрепляли с помощью связующего полимерного раствора и обрабатывали с двух сторон абразивным инструментом с тем, чтобы обеспечить пропускание газов через внутренние полости нанотрубок. Полученное таким образом устройство размером 1мм2, помещали в отпаянную стеклянную трубку с токоподводами. Для изучения сенсорных свойств этого устройства через трубку в течение 30 минут пропускали аргон с примесью NH3  или NO2 со скоростью 400 см3/мин при атмосферном давлении и комнатной температуре. Электрическое сопротивление УНТ измеряли при постоянном напряжении 1В, а также при кратковременном наложении напряжения 10В, для возвращения прибора в исходное состояние в условиях потока чистого аргона. Измерения показывают, что воздействие на прибор потока аргона со скоростью 400 см3/мин (при нормальных условиях с примесью NH3 на уровне 0,01%) приводит к увеличению его сопротивления примерно на 30%. Время срабатывания прибора составляет около 1мин. Воздействие аналогичного потока с примесью NO2 на уровне 10-5% вызывает, наоборот, снижение сопротивления на 40% при времени срабатывания 20–30с. Восстановление исходного состояния прибора происходит в течение 10 минут при пропускании потока чистого аргона и наложении постоянного напряжения 10В. Характеристики сенсора делают его приемлемым для практических применений. При этом, в отличие от других типов сенсоров на основе УНТ, в данном случае активной поверхностью сенсора является внутренняя поверхность полости нанотрубки.

А.В.Елецкий

  1. H.Y.Jung et al. Appl. Phys. Lett. 90, 153114 (2007)

Лампа накаливания на основе двухслойных углеродных нанотрубок

В первых лампах накаливания, изобретенных более 120 лет назад, в качестве источника света использовалась графитовая нить, нагреваемая под действием электрического тока до температур, при которых она испускает интенсивное оптическое излучение. Дальнейшее развитие техники привело к замене графитовой нити на вольфрамовую, которая оказалась более технологичной при изготовлении. В настоящее время лампы накаливания вытесняются более экономичными люминесцентными лампами. Однако до сих пор лампы накаливания остаются наиболее распространенными в быту, поскольку их световые характеристики лучше всего соответствуют восприятию человеческого глаза. Открытие углеродных нанотрубок (УНТ), обладающих повышенной механической, термической и химической стабильностью в сочетании с хорошими электрическими свойствами, стимулирует возможности совершенствования ламп накаливания, в которых в качестве источника света используется жгут УНТ. Детальное сравнение световых характеристик ламп накаливания на основе УНТ с традиционными источниками, в которых используется вольфрамовая нить, выполнено в одном из университетов Пекина (КНР) [1]. Двухслойные УНТ в виде пленок были синтезированы стандартным методом химического осаждения паров (CVD) с использованием в качестве исходного вещества смеси ксилола и ферроцена с добавкой серы. После проведения стандартной процедуры очистки пленку сворачивали в нити диаметром 0,06, 0,1 и 0,15 мм, которые использовали в качестве нити накаливания. Нить длиной около 20 мм подвешивали в колбе между двумя металлическими контактами, после чего колбу откачивали и отпаявали.

Светимость ламп E измеряли с помощью коммерческого прибора при различных величинах приложенного постоянного напряжения и мощности питания. На основании этих измерений вычисляли светоотдачу К, определяемую как отношение светимости к приложенной мощности Р. Результаты измерений приведены на рис., где они сравниваются с соответствующими данными для стандартной лампы накаливания с вольфрамовой нитью.

 

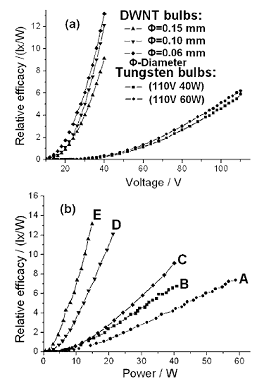Результаты сравнительных испытаний светоотдачи ламп накаливания с вольфрамовой и УНТ нитью: а) зависимость светоотдачи от приложенного напряжения; b) зависимость светоотдачи от приложенной мощности.

 

Как видно, светоотдача лампы на основе УНТ примерно вдвое превышает соответствующую величину для вольфрамового источника. Еще одной важной особенностью ламп рассматриваемого типа является сравнительно низкое напряжение питания, позволяющее использовать эти лампы на борту автомобиля или летательного аппарата. Наряду со светимостью, измеряли спектральную яркость излучения индивидуальной лампы на основе УНТ с сопротивлением 16 Ом в диапазоне длин волн 80–2500 нм. Результаты этих измерений, выполненных для различных величин цветовой температуры нитей, указывают на некоторый разброс параметра (около 2%) «произведение цветовой температуры источника на длину волны, соответствующую максимальной спектральной яркости». Отсюда следует отличие спектра излучения УНТ нити от спектра излучения абсолютно черного тела. Выполненные измерения указывают на сохранение стабильных параметров лампы накаливания с УНТ нитью в течение 3000 часов. Тем самым, выполненные исследования показывают, что лампы накаливания на основе УНТ нити во многих отношениях превосходят стандартные лампы на основе вольфрамовых нитей и могут послужить повышению конкурентоспособности ламп рассматриваемого класса.

А.В.Елецкий

  1. Q. K. Shu et al. J. Appl. Phys. 101, 084306 (2007).

СНОВА К ОСНОВАМ

Структура твердого водорода

Из всех элементов Периодической таблицы самое простое электронное строение имеет водород: в атоме водорода всего один электрон, поэтому электрон-электронное взаимодействие отсутствует. Молекула водорода H2 представляет собой простейшую систему с ковалентной межатомной связью; ее характеристики хорошо изучены экспериментально и рассчитаны теоретически с очень высокой точностью. При сильном сжатии газообразный водород переходит в твердое состояние. Теория предсказывает, что при очень высоком давлении P твердый водород становится металлом и, возможно, даже высокотемпературным сверхпроводником [1]. Экспериментально при P < 320 ГПа обнаружены три различные фазы твердого водорода, называемые фазами I, II и III – в порядке увеличения P. Все они представляют собой молекулярные кристаллы. Данные о структуре фаз II и III пока остаются неоднозначными и противоречивыми. Связано это с тем, что рентгеновская дифракция не позволяет определить ориентацию молекул H2 в твердой фазе, а нейтронографические методики по ряду причин ограничены давлениями P < 60 ГПа.

Приходится использовать косвенную информацию о частотах колебаний, которую дают рамановская и ИК спектроскопия. Эти частоты затем сравниваются с теоретическими расчетами для различных атомных конфигураций, которые, однако, берутся фактически "из головы", основываясь лишь на интуиции и "здравом смысле". При таком подходе велика вероятность "пропустить" правильную структуру, особенно если она необычная или достаточно сложная. Выбор структуры, наиболее устойчивой при данном P, осложняется еще и тем, что энтальпии различных структур очень близки друг к другу, а также необходимостью учета нулевых колебаний, вклад которых в энтальпию велик из-за малой массы атомов водорода.

Английские теоретики C.J.Pickard и R.J.Needs предложили стратегию "автоматического" численного поиска устойчивых структур твердого водорода в фазовом пространстве координат атомов [2]. Выбирая случайным образом,  начальные координаты атомов (числом от 8 до 48), заключенных в "ящик" с периодическими граничными условиями, они выполняли релаксацию системы к минимуму энтальпии путем последовательных итераций. Полная энергия рассчитывалась на каждом шаге методами теории функционала плотности (density functional theory, DFT). Стартуя с различных исходных конфигураций, авторы [2] получили большой набор структур – кандидатов в фазы твердого водорода. Затем они рассчитали для каждой из этих структур зависимость энтальпии от P вплоть до P = 400 ГПа, (нулевые колебания учитывались в гармоническом приближении). Основным результатом стало определение структуры фазы III. Она является моноклинной (пространственная группа C2/c) и представляет собой набор слоев (см. рис.), в каждом из которых имеются три неэквивалентных положения молекул H2. Оси молекул почти параллельны плоскости слоя, а их центры формируют искаженную гексагональную решетку. В элементарной ячейке 24 атома.

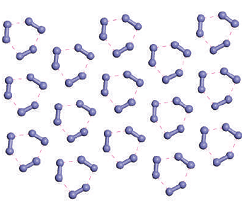
Один из слоев моноклинной структуры C2/c твердого водорода.

 

Ранее такая структура твердого водорода никем не исследовалась и даже не обсуждалась. Она термодинамически устойчива при P = (105 ¸ 270) ГПа и является диэлектрической – в соответствии с экспериментом [3] (все предыдущие структуры – претенденты на фазу III были металлическими [4]). Расчетная зависимость частот колебаний от P также хорошо согласуется с экспериментальными данными [5,6] для фазы III. Таким образом, с большой степенью уверенности можно утверждать, что фаза III имеет структуру C2/c.

Что касается фазы II, то здесь "примирить" теорию с экспериментом пока не удалось. Это связано, возможно, с тем, что в [2] не учитывались ни эффекты ангармонизма, ни поправки к адиабатическому приближению, ни квантовая  статистика протонов. Не исключено также, что все дело – в недостаточной точности использованного в [2] варианта DFT (например, DFT завышает диэлектрическую щель на (1 ¸ 2) эВ, и поэтому при обсуждении вопроса о переходе диэлектрик-металл авторы [2] вводили соответствующие поправки "руками"). В заключение отметим, что в [2] предсказаны также структуры твердого водорода при давлениях
P = (400 ¸; 500) ГПа, до которых экспериментаторы пока не добрались.

Л.Опенов

  1. N.W.Ashcroft, Phys. World 8, 43 (1995).

  2. C.J.Pickard, R.J.Needs, Nature Physics 3, 473 (2007).

  3. P.Loubeyre et al., Nature 416, 613 (2002).

  4. K.A.Johnson, N.W.Ashcroft, Nature 403, 632 (2000).

  5. R.J.Hemley et al., Europhys. Lett. 37, 403 (1997).

  6. A.F.Goncharov et al., Proc. Nat. Acad. Sci. USA, 98, 14234 (2001).

 ____________________________________________

Внимание!

С апреля 2006 г. ПерсТ выпускается только в электронном формате и представлен по адресу http://www.issp.ac.ru/journal/perst и http://perst.isssph.kiae.ru . Желающие получать выпуски ПерсТа по своему электронному адресу могут сообщить его в адрес редакции perst@issp.ras.ru

Научный редактор:  К.Кугель kugel@orc.ru

Ответственный редактор И.Чугуева  irina@issp.ras.ru тел: (495) 930 33 89, Ю.Метлин

В подготовке выпуска принимали участие:   А.Елецкий, Ю.Метлин, Л.Опенов