сверхпроводники

Антиферромагнетизм и сверхпроводимость в оксипниктидах

В работах [1] и [2], опубликованных друг за дружкой в апрельском номере Nature Materials, две научные группы сообщили об исследованиях фазовой диаграммы безмедных ВТСП REFeAsO1-xFx (RE=La в [1] и Sm в [2]) методом мюонной спектроскопии. Результаты оказались различными. Если в [1] “скачкообразное” появление сверхпроводимости наблюдалось при том же уровне допирования, при котором (также скачкообразно) исчезал антиферромагнетизм, то в [2] было обнаружено сосуществование антиферромагнитной и сверхпроводящей фаз в некотором диапазоне концентраций носителей заряда. Дело здесь, скорее всего в неоднородном распределении атомов фтора в работе [2], что приводило к фазовому расслоению на антиферромагнитные и сверхпроводящие области. Требуются новые эксперименты с более качественными образцами. А вот для RE=Ce [3] граница раздела антиферромагнетизм/сверхпроводимость на фазовой диаграмме оказалась почти такой же четкой, как и для RE=La в [1]. Это ставит под сомнение возможность наличия в оксипниктидах квантовой критической точки, поскольку последняя ассоциируется с фазовым переходом второго рода, тогда как резкое исчезновение антиферромагнетизма и наличие фазового расслоения – суть признаки перехода первого рода. В любом случае тесное соседство антиферромагнитной и сверхпроводящей фаз говорит о том, что магнитные флуктуации могут играть определенную роль в сверхпроводимости оксипниктидов.

1. H.Luetkens et al., Nature Mater. 8, 305 (2009).

2. A.J.Drew et al., Nature Mater. 8, 310 (2009).

3. Y.J.Uemura, http://arxiv.org/abs/0811.1546v2.

 

Рожденная антиферромагнетизмом

Для возникновения сверхпроводимости требуется наличие эффективного притяжения между электронами. Оно приводит к формированию куперовских пар, которые образуют конденсат, способный двигаться по кристаллической решетке без сопротивления. Теория БКШ объясняет, как в простых металлах и сплавах притяжение за счет обмена виртуальными фононами пересиливает межэлектронное кулоновское отталкивание. Физический механизм притяжения электронов в ВТСП (как купратных, так и безмедных) пока остается предметом дискуссий. Не исключено, что он является нефононным. Анализ экспериментальных данных осложняется наличием в ВТСП различных электронных неоднородностей. Существует даже точка зрения, что именно в этих неоднородностях нужно искать ключ к высокотемпературной сверхпроводимости.

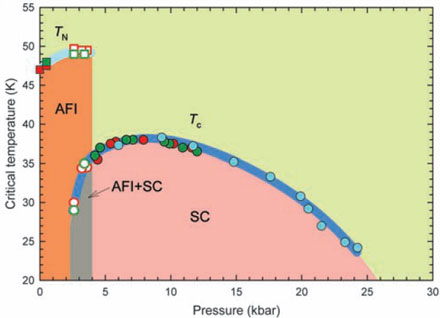
Фазовая диаграмма Cs3C60 в координатах Tc–P.

 

Еще один класс сверхпроводников представляют фуллериды A3C60 (A = щелочной металл) с ГЦК структурой. До сих пор считалось, что монотонный рост их критической температуры Tc до 33 К при увеличении радиуса ионов A+ (и соответствующем увеличении расстояния между молекулами C60) находит естественное объяснение в моделях а-ля БКШ, согласно которым Tc определяется величиной плотности электронных состояний на уровне Ферми N(eF). В отличие от ВТСП, в ГЦК-фуллеридах отсутствует диэлектрическое состояние, конкурирующее со сверхпроводящим. В работе [1] сообщается о наличии такого состояния в фуллериде Cs3C60 со структурой А15. При атмосферном давлении P этот фуллерид является антиферромагнитным диэлектриком (температура Нееля TN = 46 К), а при гидростатическом сжатии становится сверхпроводником (см. рис.), причем антиферромагнитная и сверхпроводящая области на фазовой диаграмме не разделены (как в ВТСП), а перекрываются, то есть сверхпроводящее состояние “рождается” непосредственно из антиферромагнитного. При этом немонотонная зависимость Tc от P (и, соответственно, от N(eF)) не укладывается в схему БКШ. Авторы [1] подчеркивают, что структурные и электронные неоднородности в Cs3C60 со структурой А15 отсутствуют. Они полагают, что этот фуллерид может стать “полигоном” для выявления взаимодействий, приводящих к сверхпроводимости сильнокоррелированных систем. И эти взаимодействия вполне могут оказаться электронными.

Л.Опенов

1. Y.Takabayashi et al., Science 323, 1585 (2009).

 

НАНОСТРУКТУРЫ, НАНОТЕХНОЛОГИИ, НАНОЭЛЕКТРОНИКА

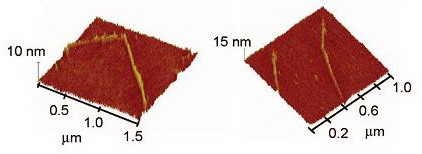
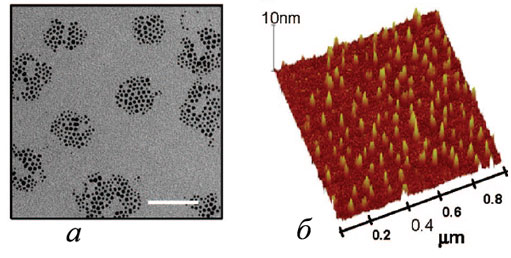
Шаблоны из диацетилена для наноструктур золота

Создание организованных наноструктур является одним из основных направлений современных нанотехнологий. Для решения поставленных задач применяются различные методики и подходы. Авторы работы [1] предлагают использовать изотермически сжатые на границе раздела воздух/вода мономеры диацетилена в качестве шаблонов для получения различных поверхностных архитектур организованных наноструктур золота. В частности, они показали, что упорядоченные золотые наночастицы, покрытые алкилтиолом могут быть сформированы при помощи диацетиленовых пленок. Изготовленные подобным способом образцы затем легко переносят с поверхности воды на твердую подложку, а органический шаблон полностью удаляют посредством плазменного травления, при этом наночастицы сохраняют сложившееся упорядочение. Более того, авторам удалось обнаружить зависимость между молекулярным составом мономеров диацетилена и организацией золотых наночастиц. В работе использовали диацетилены с одной и двумя карбоксильными группами. Анализ получившихся в эксперименте наноструктур золота с помощью атомно-силовой и просвечивающей электронной микроскопии показал, что в зависимости от используемого шаблона имеет место различная организация: так при использовании диацетилена с одной карбоксильной группой наблюдали “ленты” (рис. 1), а при использовании диацетилена с двумя карбоксильными группами – “островки” (рис. 2).

Рис. 1. Наночастицы золота, внедренные в шаблон из диацетилена с одной карбоксильной группой. Изображения, полученные с помощью атомно-силового микроскопа после плазменного травления.

Рис. 2. Наночастицы золота, внедренные в шаблон из диацетилена с двумя карбоксильными группами: а - изображение, полученное с помощью просвечивающего электронного микроскопа (шкала соответствует 50 нм); б - изображение, полученное с помощью атомно-силового микроскопа после плазменного травления.

Таким образом, учитывая достижения современных методов синтеза мономеров диацетилена, описанный в работе [1] способ окажется, несомненно, полезным при изготовлении различных упорядоченных наноструктур.

М.Маслов

1. N.Markovich et al., J. Am. Chem. Soc. 131, 2430 (2009).

КВАНТОВЫЕ СИСТЕМЫ

Ферми-конденсатный фазовый переход кардинально меняет ферми-жидкость

К сильнокоррелированным ферми-системам (СФС) – одному из объектов пристального внимания современной фундаментальной физики – относятся высокотемпературные сверхпроводники (ВТСП), металлы с тяжелыми фермионами (ТФ) и ряд двумерных (2D) ферми-систем. Несмотря на то, что СФС достаточно хорошо изучены экспериментально, пока для нас во многом остаются загадкой физические причины их необычного поведения. Свойства СФС не укладываются в привычную картину ферми-жидкости и не имеют общепринятого теоретического объяснения. К настоящему времени предложено много совершенно различных подходов к описанию СФС. Какой из них правильный, покажет время. В этой заметке мы хотим обратить внимание читателей ПерсТа на концепцию так называемого ферми-конденсатного квантового фазового перехода (ФККФП), которая, по нашему мнению, позволяет с единой точки зрения объяснить многие особенности СФС.

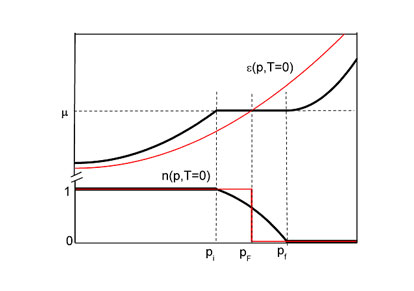
Рис. 1. Функция распред"еления квазичастиц n(p,T=0) и одночастичный спектр ε(p,T=0). Красные линии – до ФККФП, черные линии – после ФККФП. 

При описании СФС ключевым понятием является квантовый фазовый переход, имеющий место в критической точке при T=0 [1]. Экспериментальные данные указывают на очень большую эффективную массу M* квазичастиц в СФС и даже на ее расходимость в критической точке. Мы считаем, что такое поведение уместно связать с ферми-конденсатным квантовым фазовым переходом (ФККФП), характеризующимся неограниченным ростом M* в критической точке [2].

Как видно из рис. 1, при ФККФП форма функции распределения квазичастиц становится отличной от привычной фермиевской ступеньки, и поверхность Ферми при p=pf размывается, превращаясь в “ферми-объем”, заполненный квазичастицами с импульсами pi<p<pf. Спектр в этом интервале становится абсолютно плоским, а M* обращается в бесконечность. Занимающие этот ферми-объем квазичастицы с М*=∞ образуют новую фазу, получившую название “фермионный конденсат”. Таким образом, после ФККФП ферми-система состоит из двух подсистем: обычных квазичастиц Ландау (р<рi) и ферми-конденсата (pi<p<pf). При T¹0 плоский участок спектра перестает быть строго горизонтальным, и масса M* становится конечной. Поэтому ферми-конденсатный фазовый переход является квантовым и происходит при изменении не температуры, а давления P, магнитного поля B, плотности частиц x и т. п. Для ФККФП справедлива расширенная парадигма Ландау, согласно которой квазичастицы по-прежнему определяют низкотемпературные свойства ферми-системы, но их масса M* уже не постоянна, а зависит от P, B, x, T и других внешних параметров, что и приводит к не-ферми-жидкостному поведению СФС [2]. Так как масса M* входит в различные термодинамические характеристики ферми-системы (например, энтропия, магнитная восприимчивость и теплоемкость пропорциональны M*), то универсальность температурной зависимости M*, о которой речь пойдет ниже, диктует и универсальность поведения различных СФС. Транспортные свойства также определяются величиной M*. Например, измерение удельного сопротивления ρ=ρ0+AT2 как функции температуры позволяет найти транспортный коэффициент A~(M*)2 и выявить таким образом универсальные свойства магнетосопротивления в металлах с ТФ.

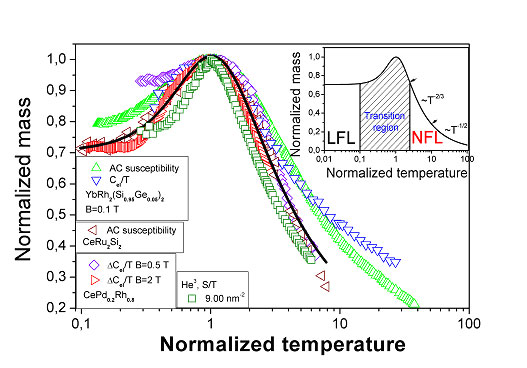Рис. 2. Универсальная зависимость нормированной эффективной массы M*N от нормированной температуры TN, определенная путем измерений магнитной восприимчивости YbRh2(Si0.95Ge0.05)2 и CeRu2Si2 [4,5], теплоемкости YbRh2(Si0.95Ge0.05)2 и CePd0.2Rh0.8 [4,6] и энтропии 2D 3He [7]. Сплошная линия – теоретическая зависимость [3]. На вставке заштрихована область, являющаяся переходной от ферми-жидкостного (LFL) к не-ферми-жидкостному (NFL) поведению.

На вставке к рис. 2 приведены результаты расчетов температурной зависимости M* в постоянном внешнем магнитном поле B для модели однородной электронной жидкости, находящейся в критической точке ФККФП [3]. При B=0 масса M* в критической точке расходится, но магнитное поле возвращает систему в состояние ферми-жидкости Ландау. С ростом температуры это состояние разрушается, а величина M* достигает максимума MM~B-2/3 при некоторой температуре TM~B и затем уменьшается при переходе в не-ферми-жидкостное состояние (MM→∞ и TM→0 при B→0). Поскольку система находится вблизи ФККФП, то характерными масштабами массы M* и температуры T являются MM и TM, соответственно. Зависимость нормированной эффективной массы M*N=M*/MM от нормированной температуры TN=T/TM приведена на вставке к рис. 2. Видно, что M*N зависит только от TN, но не от магнитного поля, то есть зависимость M*N(TN) является универсальной. Экспериментальные данные для различных СФС хорошо согласуются с теорией ФККФП [3] (рис. 2). Поскольку величина M* является функцией температуры, магнитного поля, плотности (для 2D 3He), химического состава (для металлов с ТФ) и, вообще говоря, мерности системы (2D 3He – двумерная система, а металлы с ТФ – трехмерные), то демонстрация универсальной зависимости M*N от TN (рис. 2) является замечательным достижением теории СФС, основанной на концепции ФККФП.

На рис. 3 приведены результаты измерения транспортного коэффициента A в YbRh2Si2 [8] и ВТСП Tl2Ba2CuO6+x [9]. На вставке изображена зависимость нормированного коэффициента AN=A/A0 от нормированного магнитного поля B/Bc0 (здесь A0 – независящая от B составляющая коэффициента A, а Bc0 – критическое поле, при котором происходит переход в парамагнитную фазу [8-10]). Как видно из вставки, зависимость AN от B/Bc0 также является универсальной. Отметим, что на данный момент только теория СФС, основанная на ФККФП, позволяет описать это универсальное поведение.

 

Рис. 3. Транспортный коэффициент A как функция магнитного поля B. Экспериментальные данные для YbRh2Si2 (квадраты) [8] и ВТСП Tl2Ba2CuO6+x (кружки) [9]. На вставке приведены нормированные значения A/A0 как функции нормированного магнитного поля B/Bc0. Сплошные линии – результаты расчета [10].

Рис. 4. Температурные зависимости магнетосопротивления CeCoIn5 в различных магнитных полях B. Символы – экспериментальные данные [11]. Сплошные линии – результаты расчета [10].

 

На рис. 4. показаны температурные зависимости магнетосопротивления (MR) CeCoIn5 в различных полях [11]. Видно, что при низких температурах MR отрицательно, а с ростом T становится положительным, достигает максимума и затем вновь убывает. Такое поведение MR обусловлено опять же универсальной зависимостью эффективной массы M*N от TN (рис. 2) и пока находит объяснение только в рамках теории ФККФП [10].

К.Г. Попов, В.Р. Шагинян

1. P.Gegenwart et al., Nature Phys. 4, 186 (2008).

2. В.Р.Шагинян, М.Я.Амусья, К.Г.Попов, УФН 177, 585 (2007); V.A.Khodel et al., Phys. Rev. B 78, 075120 (2008).

3. V.R.Shaginyan et al., Phys. Rev. Lett. 100, 096406 (2008).

4. J.Custers et al., Nature  424, 524 (2003).

5. D.Takahashi et al., Phys. Rev. B 67, 180407(R) (2003).

6. A.P.Pikul et al., J. Phys.: Condens. Matter 18, L535 (2006).

7. M.Neumann et al., Science 317, 1356 (2007).

8. P.Gegenwart et al., Phys. Rev. Lett. 89, 056402 (2002).

9. T.Shibauchi et al., Proc. Natl. Acad. Sci. USA 105, 7120 (2008).

10. V.R.Shaginyan et al., Phys. Lett. A 373, 686 (2009); V.R.Shaginyan et al., Phys. Lett. A 373, 986 (2009).

11. J.Paglione et al., Phys. Rev. Lett. 91, 246405 (2003).

МИКРОТЕХНОЛОГИИ

Корпорация монстров и законы природы

Комментарий на сайте www.physicsworld.com под броским заглавием “Energy harvesting from human vibrations” к статье [1] вызвал у меня воспоминания об умном, добром и очень изобретательном мультфильме “Корпорация монстров”, в котором некая корпорация добывает энергию из детских отрицательных эмоций, из страхов, визгов и т.п. И, уж совсем некстати, я стал подсчитывать, сколько батареек можно было бы зарядить от энергии вибраций научных работников, услышавших от Ирины Ясиной [2] размер зарплат т.н. “топ-менеджеров” научно-технологических госкорпораций (млн. руб. в месяц!). Жаль, конечно, что эксперт-экономист Ясина сравнила ее с меньшей месячной зарплатой министров, а не с гораздо меньшим годовым объемом финансирования научных грантов (не будем, кстати, проводить сравнение с зарплатой исполнителей этих грантов – в этом случае выделяемая энергия не поддается исчислению в принятых единицах). Но это лирика. А вот сама тема, затронутая в упомянутой статье итальянских авторов (Univ. Perugia), чрезвычайно важна, особенно, в свете предсказываемых провидцами-фантастами энергетических войн.

Мысль о том, что человек не только венец творения, но и источник электроэнергии с очень приличным КПД, появляется не впервые. В последние десятилетия чаще других прорабатывался вопрос автономного снабжения электричеством отдельного индивидуума, естественно, преимущественно в интересах военных или для целей выживания. Отзвуки этих разработок появились у нас в быту, в виде нового поколения мини-динамо-машинок для фонарей или зарядок для телефонов.

Придумано и сделано много всякого. Например, автономное устройство для бойца, который не должен выпускать из рук автомат. В этом случае генерирующим устройством является обувная стелька с пьезоэффектом. А чтобы провода не мешали движению, предложено преобразовывать электроэнергию в высокочастотные колебания и передавать ее из ботинок на высоту торса без проводов. Эхо этих разработок также недавно проникло в гражданскую среду и с полгода блуждало по околонаучному интернету под слоганом “передача энергии без проводов”.

Однако такие же разработки нужны и для сугубо гуманных целей – например для медицины. Нанотехнологи планируют создать микророботы, которые будут осуществлять диагностику органов или, может быть, даже коррекцию отдельных недостатков внутри нас, людей. Как питать электричеством этих роботов? Тянуть провода, как за ПТУРС’ом*, или заглатывать батарейки?

В восьмидесятые годы (еще до нанотехнологического бума) именно для этой ситуации было предложено красивое high-tech решение. В человеческой крови есть глюкоза и связаный кислород. В принципе это позволяет создать сверхминиатюрный топливный элемент, встроенный в кровеносный сосуд. Конкурируя с собственным обменом организма, такой топливный элемент, конечно, будет являться в некотором смысле паразитом, но если при этом он сможет питать кардиостимулятор или какой-то жизненно необходимый датчик, такое решение было бы приемлемым.

Собственно, именно эта задача – обеспечение электропитания микроустройств за счет возможностей человека - анонсирована во вводной части обсуждаемой статьи в Phys.Rev.Lett. А как раз дальше начинаются законы природы.

Именно эти законы оставляют не так много вариантов решений поставленной задачи. Конечно, человек теплее окружающей среды, но, согласно второму закону термодинамики, устройство, находящееся внутри человека, это тепло использовать не может. Но зато человек шевелится! Даже спящий он ворочается с бока на бок, у него пульсирует кровь, поднимается и опадает грудная клетка. Авторы сразу ориентируются на этот путь и намереваются внедрить куда-то в нас пьезоволокна, которые будут собирать энергию из микродвижений. Далее в статье констатируется, что и шевелится-то человек кое-как: - частоты не фиксированы, энергия размыта по спектру, резонансного отбора энергии (как в упомянутом материале про передачу без проводов) не организовать.

Тут-то авторы выкладывают главный козырь: если энергия размыта по спектру, то пусть ее поглощает нелинейный осциллятор, у которого нет фиксированной резонансной частоты, а нелинейный колебательный режим раскладывается на широкую область частот. В доказательство правильности этой идеи авторы сооружают автогенератор с регулируемой нелинейностью и получают, что амплитуда колебаний тем больше, чем больше нелинейность.

Правда, в одном месте авторы оговариваются – “…соответствующим образом организованный осциллятор”. И за этим стоит многое. Пытаться за счет нелинейности осциллятора получить более интенсивной отбор энергии от равновесного резервуара - значит действовать вопреки законам природы. Пример простой: приведем два осциллятора (линейный и нелинейный) в контакт с термостатом. В общем случае нелинейный осциллятор – осциллятор, собственная частота колебаний которого зависит от амплитуды. Но в термостате на каждую степень свободы приходится одна и та же энергия. Следовательно, при любой амплитуде энергия, приходящая на осциллятор, одна и та же. Можно даже, чтобы показать связь этого с законами природы, достроить рассуждение воображаемой тепловой машиной, которая будет совершать работу, передавая энергию от нелинейного осциллятора в линейный, нарушая второй закон термодинамики. И с очевидностью подытожить – нелинейная система не будет потреблять больше энергии от термостатированного резервуара, чем линейная.

Тогда в чем же смысл статьи? На самом деле авторы создали не только нелинейный осциллятор, но и систему, которая эффективно накачивает в него энергию именно в таком режиме. В этом смысл нечаянной оговорки авторов – “...и такая система действительно эффективно потребляет энергию”. Что именно нетривиального увидела редакция Phys.Rev.Lett, - кто знает? Это скрыто за тонкостями перевода.

Разве что еще одна аналогия с делами общечеловеческими. Созданная система работает по специально для нее созданным правилам отбора энергии. Удивительно ли, что она отбирает энергию эффективнее других? Подобных примеров много, и большинство из них – вне физики.

Замечательный все-таки журнал Physical Review Letters! Статья не видная, эксперимент на уровне лабораторной работы, выводы и вовсе сомнительные – а вот поди ж ты – сколько интересных поворотов темы сумели затронуть своей статьей!

______________________

*ПТУРС – противотанковый управляемый ракетный снаряд

М.Компан

1. Phys. Rev. Lett., 102, 080601 (2009).

2. http://www.echo.msk.ru/blog/yasina/580251-echo/

МАТЕРИАЛОВЕДЕНИЕ

Сегнетоэлектрические доменные границы в роли проводов

В прошлом номере мы писали о том, как доменные стенки в сегнетоэлектриках способны вызывать магнитные неоднородности [1], а немногим ранее – об электрических свойствах магнитных доменных границ [2]. Теперь же сегнетоэлектрические доменные границы преподнесли новый сюрприз – в непроводящем диэлектрике они становятся проводящими каналами [3].

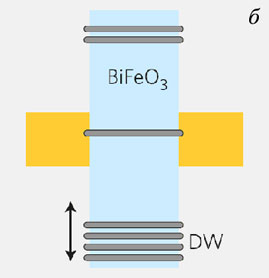
Это явление было замечено при сканировании поверхности сегнетоэлектрика феррита висмута BiFeO3 при помощи зондового микроскопа в резистивной моде. В этом режиме измерений по напряжению между образцом и зондом, касающимся поверхности, и току, протекающему через иглу зонда, определяют сопротивление участков образца, расположенных непосредственно под иглой (рис. 1а). Удельное сопротивление доменной границы составляло всего 1-10 Ом•м, что на пять-шесть порядков меньше сопротивления диэлектрического окружения.

В качестве предполагаемых причин возникновения проводимости в области доменных границ авторы выделяют два явления: 1) потенциальный барьер вблизи границы и, как следствие, повышенной концентрацию носителей заряда в этой области (избыточная электрическая поляризация доменной границы ΔP~10 мКл/см2 около 10% от величины поляризации в доменах) 2) уменьшение ширины запрещенной зоны в полупроводнике BiFeO3 на 10% (около 0.1 эВ).

 

Рис. 1. Проводящие доменные границы в сегнетоэлектрике феррите висмута BiFeO3
 а - схематическое изображение измерений с помощью зондового микроскопа в резистивной моде;
 б - использование доменных границ (DW) в качестве проводящих каналов, число и положение которых управляется электрическим полем [4].

Доменные границы, как объекты существенно наноскопические (характерная толщина ~1нм) и обладающие дополнительными функциональными свойствами по сравнению с областями с однородным распределением поляризации (доменами), представляют несомненный интерес для практических применений. Примером тому может служить схема устройства, предложенного в [4]: доменные границы служат проводящими мостиками между двумя электродами (желтые области рис. 1б), которые можно перемещать внешним воздействием (электрическим полем или током), подобно тому, как это делается в «памяти на беговой дорожке» [1]. Примечательно, что феррит висмута помимо ярко выраженных сегнетоэлектрических свойств является еще и мультиферроиком, т.е. электрическое упорядочение в нем соседствует с магнитным, а сегнетоэлектрические доменные границы, по совместительству, могут быть еще и  магнитными. Последнее делает феррит висмута поистине универсальным материалом для создания многофункциональных элементов микроэлектроники.

А. Пятаков

1. ПерсТ 15, вып. 23, с. 3 (2008).

2. ПерсТ 16, вып. 6, c.5 (2009).

3. J. Seidel et al, Nature Mater. 8, 229 (2009).

4. H. Béa and P. Paruch, Nature Mater. 8, 168 (2009).

 

СПИНТРОНИКА

Фильтр для запутанности

Свойство запутанности присуще только квантовым частицам. Именно на основе запутанности состояний кубитов в квантовом компьютере возможно экспоненциальное ускорение некоторых важных алгоритмов. На запутанности основана и квантовая коммуникация. Серьезной проблемой в квантовой коммуникации является затухание, которое ограничивает достижимое расстояние величиной около 150 км. Для больших расстояний требуются квантовые повторители: необходимо передать состояние «старого» фотона на «свежий» фотон, который и пойдет дальше. Есть и совершенно неожиданное применение запутанности: запутывание фотонов снижает диффракционный предел фотолитографии.

Пока идут дискуссии о введении меры запутанности состояния многих частиц, ученые придумывают установки, которые бы служили фильтрами для запутанных и незапутанных частиц. Сейчас речь идет только о двух фотонах. На рис. 1А показан принцип работы обычного поляризационного фильтра для одиночных фотонов. Он пропускает фотоны только вертикальной поляризации. Фильтр на рис. 1В пропускает пары фотонов только тогда, когда оба фотона имеют одинаковую поляризацию: либо горизонтальную, либо вертикальную. Если через такой фильтр пропустить два фотона с диагональной поляризацией, то они непременно запутаются (рис. 1С). Таким образом, фильтр пропускает либо исходно запутанное состояние, либо делает его таковым. Этот фильтр был предложен в 2002 году [1]. Авторы работы [2] модифицировали фильтр с помощью применения некоторых новых оптических элементов, например, частичного поляризатора.

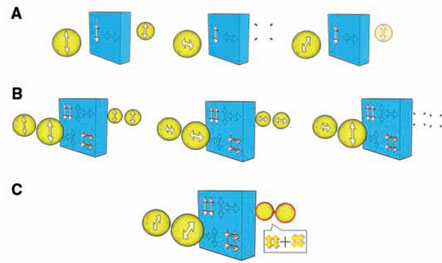
Рис. 1. Принцип действия поляризационного фильтра для одиночных фотонов (А), для двух фотонов (В) и запутывание двух фотонов с диагональной поляризацией (С).

Схема установки слишком сложна. Мы не решаемся ее привести, чтобы не отпугнуть читателей, но основной принцип ее проектирования назовем. Обычно запутанность между частицами возникает в результате их взаимодействия. Обеспечить эффективное взаимодействие фотонов пока не удается, поэтому в устройствах применяют только линейные оптические элементы. Для создания нелинейности, приводящей к запутанности, используют свойство тождественности фотонов. Их можно считать тождественными, если они имеют очень близкую энергию. Далее их нужно одновременно пропустить по одному пути. На выходе надо поставить 50% делитель, который половину фотонов пропускает вперед, а половину отражает в перпендикулярном направлении. Само по себе это еще не приводит к запутанности фотонов. Чтобы получить запутанность, необходимо убедиться, что фотоны пошли разными путями, иными словами, надо зарегистрировать прохождение какого-то фотона по одному пути и какого-то фотона по другому пути. Здесь слово «какого-то» является ключевым для понимания явления, оно и отражает тождественность частиц. К сожалению, все современные методы подобного измерения состояния фотонов приводят к их гибели в тот момент, когда срабатывают счетчики фотонов, установленные в плечах интерферометра. Это вызывает необходимость использования вспомогательных фотонов, которые и измеряются, а основные фотоны летят дальше. Соответственно, в устройстве фильтра двухфотонной запутанности (рис. 1В) используется два вспомогательных фотона. Как мы видим, рассмотренный фильтр требует источников одиночных идентичных фотонов, причем, эти источники должны быть с очень высокой точностью синхронизированы.

В.Вьюрков

1. H.F.Hofmann et al., Phys. Rev. Lett. 88, 147901 (2002).

2. R.Okamoto et al., Science 323, 483 (2009).

ФУЛЛЕРЕНЫ И НАНОТРУБКИ

Углеродные нанотрубки – основа для новых нейроэлектродов

Благодаря уникальной комбинации физических, электрических, механических и оптических свойств углеродные нанотрубки являются одним из самых перспективных материалов для нейроэлектродов, в том числе имплантируемых в мозг человека [1,2].

Исследования человеческого мозга – его организации и функционирования – ведутся во многих лабораториях мира. Используются различные современные методы, в том числе позитронно-эмиссионная и магнитно-резонансная томографии, однако самые большие успехи в познании мозга до настоящего времени были связаны с применением имплантированных электродов, то есть в условиях непосредственного контакта с мозгом человека. Да и сейчас электростимуляция с помощью имплантированных электродов является основой для исследования, диагностики и лечения [3,4].

Первым эту методику применил еще в 1920-е годы Уолтер Рудольф Гесс (Walter Rudolf Hess), швейцарский физиолог, лауреат Нобелевской премии по физиологии и медицине 1949 г. Он имплантировал проволочные электроды в мозг кошек и проводил электростимуляцию, которая влияла не только на движение кошек, что ожидалось, но и на их настроение [4]. В последующие десятилетия многие исследователи стали использовать имплантированные электроды. Широко известны работы физиолога испанского происхождения Хосе Дельгадо (Jose Delgado). В 1950-60-ых гг. он имплантировал кошкам, обезьянам, быкам и другим животным сначала электроды с проводами, а затем и разработанные им приемники радиосигналов (кстати, одно из его других изобретений – прототип сердечного стимулятора). Дельгадо также устанавливал электроды в мозг безнадежным пациентам, страдавшим тяжелыми формами шизофрении и эпилепсии, не поддающимися лечению другими способами. В нашей стране в этом направлении первыми стали работать академик Н.П. Бехтерева и её сотрудники; в 1960-70 гг. в тяжелых случаях они иногда вживляли электроды больным паркинсонизмом, эпилепсией для лечебной стимуляции [3]. После нескольких лет клинических испытаний в 1997 г. нейростимуляторы компании Medtronic были одобрены для лечения больных паркинсонизмом. Эти стимуляторы имеются на рынке под торговыми марками Soletra и Kinetra. Сейчас в мире более 30 000 человек с нарушениями двигательных функций имеют имплантированные в мозг электроды (соединенные проводами с устройством, имплантированным под кожу рядом с ключицей) [4]. Аналогичные стимуляторы в 2005 г. одобрены в США для лечения депрессии; в 2009 г. начаты клинические испытания глубокой стимуляции мозга для лечения ожирения; ожидается появление имплантируемых устройств, которые помогут видеть полностью слепым.

Однако для широкого распространения этого метода лечения и повышения его эффективности и надежности необходимо решить ряд вопросов. Новейшие устройства должны будут состоять из множества электродов, поэтому потребуется уменьшить их размеры, создать наноэлектроды. Традиционные материалы не позволяют это сделать. Вторая проблема – биосовместимость. Как правило, большинство электродов в реальных условиях работают лишь несколько месяцев, в редких исключениях – несколько лет. Возможны отдаленные воспалительные эффекты, деградация тонких металлических электродов.

Существуют различные подходы к улучшению биосовместимости и созданию электродов, способных взаимодействовать с отдельными нейронами. Некоторые результаты использования углеродных нанотрубок для изучения роста и организации нейронной сети, улучшения эффективности передачи сигналов в нервной системе уже были описаны в ПерсТе [2]. Американские исследователи [1] сделали новые важные шаги на пути создания эффективных нейроэлектродов. Они определили три необходимых направления работ:

1) использование электрических и механических свойств новых наноструктурированных материалов, включая композиты на основе углеродных нанотрубок – это повысит долговечность и позволит уменьшить размеры;

2) введение в электроды нервных стволовых клеток, из которых в поврежденных областях могут образоваться функциональные нейроны – это может заметно снизить воспаления в нервной ткани;

3) достижение лучшей интеграции тканей и электродов путем «гуманизации» материала – то есть путем изготовления материала, структурно и химически наиболее близкого к живой ткани вокруг нейронов.

Детальная оценка всех этих подходов займет, по мнению авторов, несколько лет, так как кроме лабораторных исследований потребуются эксперименты на животных. А пока в статье [1] они продемонстрировали техническую возможность изготовления электродов, удовлетворяющих этим требованиям.

Исследователи создали композиты из чередующихся слоев одностенных углеродных нанотрубок (ОСНТ) и ламинина - белка, входящего в соединительную ткань человека. Этот важный адгезивный белок обеспечивает фиксацию клеток; он часто применяется в биологических исследованиях в качестве покрытия. В работе [1] был применен метод послойной сборки, который обеспечивает высокий уровень контроля и возможность управления свойствами, а кроме того – механическую прочность (рис.1). Ранее и другие исследователи таким способом получали композиты для изучения нервных клеток, но наряду с ОСНТ использовали синтетические небиологические полимеры. В отличие от этого предложенные в [1] послойные композиты из нанотрубок и природного полимера ламинина сочетают свойства как биосовместимого субстрата, обеспечивающего адгезию и развитие нервных клеток, так и электропроводной подложки для стимуляции.

Рис.1. Данные атомно-силовой микроскопии: а) монослой ламинина на SiO2 подложке, b) 6 двойных слоев ОСНТ/ламинин (шкала – 1 мкм).

Авторы [1] сделали композиты из разного числа двойных слоев ОСНТ/ламинин (до 30) и изучили на этих подложках адгезию нервных стволовых клеток в зависимости от ряда параметров (число слоев, их последовательность, состав последнего слоя, термообработка и др.). Наилучшие результаты были получены для композита, верхний слой которого состоял из ОСНТ, причем после непродолжительной термообработки (10 мин., 300оС). Возможно, это связано с тем, что термообработка придает гелеподобным слоям ламинина необходимую жесткость (при этом слои ОСНТ препятствуют полному разрушению их структуры). Удельная электропроводность композита из 10 двойных слоев составила 430 и 2140 См/м до и после термообработки, соответственно. Была подтверждена не только адгезия стволовых нервных клеток, но и их последующая так называемая дифференциация - трансформация в различные клетки нервной системы. Наблюдался рост нейронов (рис.2), 98% клеток были жизнеспособны (рис.3).

Рис.2. Рост нервных клеток на субстрате из чистого ламинина и композита из ОСНТ/ламинин после термообработки: желтый цвет через 24 ч.,
красный – через 48 ч. голубой – через 72 ч., зеленый – через 120 ч.

Рис.3. Жизнеспособность клеток на ОСНТ/ламинин подложке. Живые клетки показаны зеленым цветом, мертвые – красным. Шкала – 200 мкм.

Была зарегистрирована синаптическая активность, указывающая на формирование действующей сети нервных клеток. Электростимуляция (рис.4) привела к возникновению «потенциалов действия» (см. [2]). Для детектирования был использован флуоресцентный метод.

Таким образом, американские ученые показали, что композит белок – ОСНТ может служить основой электродов нового типа, которые: 1) включают ОСНТ как превосходный проводник и упрочняющий компонент, 2) способствуют развитию нервных клеток и формированию действующей сети, 3) позволяют проводить электростимуляцию стволовых нервных клеток и продуктов их дифференциации. Этот материал химически близок к живой ткани, так что можно надеяться на его долговечность, что особенно существенно для нейропротезирования.

Рис.4. Устройство для электростимуляции клеток. Два кольца (камеры для клеток и жидкой среды) помещены на многослойную композитную пленку; провода присоединены к области ОСНТ при помощи серебряной пасты и медной ленты.

 

Трудно отрицать важность этих и других подобных экспериментов. Но, наверное, каждый из нас задумывается над тем, к чему они могут привести. Возможно ли злоупотребление нейротехнологическими методами?.. Как пишет автор [4], в США работы по созданию интерфейса мозг – внешнее устройство в основном финансируются военными. Среди ученых всегда находились яростные противники внедрения электродов в мозг. Ведь, как было сказано выше,  даже в первых опытах Гесса у кошек менялось настроение, и первоначально добродушное животное могло стать агрессивным. Не удивляет и неоднозначное отношение к работам Дельгадо, - у его пациентов стимуляция мозга могла вызвать страх, веселье, или злобу, иногда эмоции были очень сильными. При этом пациенты искренне верили, что это естественное проявление, никак не связанное с воздействием на мозг. Своим противникам Дельгадо заявлял, что невозможно запретить приобретение знаний, как невозможно и остановить прогресс. Остается надеяться, что ученые, технологи и политики будут следовать заключению Европейской группы по этике в науке и новых технологиях, принятому в 2005 г.: «Этическое понятие неприкосновенности человеческого тела не должно быть понято как барьер для развития науки и техники, но как барьер для их возможного неправильного применения» [5].

О.Алексеева

1. N.W.-S.Kam et al., Nanolett. 9, 273(2009).

2. ПерсТ 16, вып.5. с.5 (2009).

3. Н.П.Бехтерева. Магия мозга и лабиринты жизни. – М.: АСТ (2007).

4. A.Keiper, New Atlantis, № 11, 4 (2006).  http://www.thenewatlantis.com/publications/the-age-of-neuroelectronics

5. http://ec.europa.eu/european_group_ethics/docs/avis20_en.pdf

Самая узкая металлическая нанотрубка

Давно известны и активно исследуются углеродные нанотрубки (УНТ) – свернутые в трубку графитовые слои. Гораздо меньше информации о нанотрубках из других химических элементов. Бразильские ученые изготовили нанотрубки из серебра [1]. В отличие от своих углеродных старших сестер они имеют не круглое, а квадратное поперечное сечение. Такие нанотрубки спонтанно формируются при удлинении серебряных наноконтактов, о чем свидетельствуют данные просвечивающей электронной микроскопии высокого разрешения (HRTEM), см. рис.

 

Процесс образования нанотрубки при удлинении серебряного нанопровода (изображения получены методом HRTEM). 

Их толщина составляет всего один период решетки (около 4 ангстрем)! Однако у авторов [1] возникло сомнение: а действительно ли это “чисто серебряные” нанотрубки? Какой пробы у них серебро? Ведь HRTEM не видит легких элементов (таких как, например, водород и углерод). Может быть, именно их примеси стабилизируют “наноквадратную” структуру трубки? Но расчеты из первых принципов, выполненные в рамках теории функционала плотности, показали, что именно такая структура отвечает минимуму энергии. Для баллистической проводимости серебряных нанотрубок теория предсказывает величину около 3.6G0, где G0 – квант проводимости. Что ж, на поле наноэлектроники у УНТ появился достойный конкурент…

Л.Опенов

 

1. M.J.Lagos et al., Nature Nanotech. 4, 149 (2009).

 

КОНФЕРЕНЦИИ

Научная сессия ОФН РАН “Наноплазмоника и метаматериалы”
27 апреля 2009г., (14.00)

(Ленинский просп., 53, конференц-зал)

Программа

1. Тиходеев С.Г. (ИОФ РАН) - Плазмон-поляритонные эффекты в наноструктурированных металл-диэлектрических фотонных кристаллах и метаматериалах

2. Шубина Т.В., Иванов С.В., Торопов А.А., Копьев П.С. (ФТИ РАН) - Плазмонные эффекты в наноструктурах на основе In(Ga)N

3. Курин В.В. (ИФМ РАН) - Резонансное рассеяние света на наноструктурированных металлических и ферромагнитных пленках

4. Лагарьков А.Н., Сарычев А.К. (ИТПЭ ОИВТ РАН) - Активные оптические метаматериалы

5. Гиппиус Н.А. (ИОФ РАН) - Применение метода матрицы рассеяния для расчета оптических свойств метаматериалов металл/диэлектрик

Web: http://www.gpad.ac.ru/

 

II Междисциплинарный, международный симпозиум
“Плавление-кристаллизация металлов и оксидов” (MCMO-2009),
5-9 сентября 2009, Ростов-на-Дону, п. Лоо

Тематика

1.        Жидкое состояние однокомпонентных и многокомпонентных систем.

2.        Теория плавления и состояния расплавов (статистическая физика, модели, компьютерные расчеты)

3.        Расслоение расплавов и твердых растворов, физика двухфазных состояний.

4.        Фазовые диаграммы (эксперимент и теория).

5.        Плотноупакованные структуры, реконструктивные фазовые переходы, переход мартенсит-аустенит

6.        Плавление стекол, аморфных и наноструктурированных сплавов.

7.        Природа, структура и свойства эвтектик. Равновесное и неравновесное плавление – кристаллизация сплавов эвтектического состава.

8.        Низкоразмерные фазовые переходы (плавление-кристаллизация при контакте разнородных веществ).

9.        Плавление наноструктурированных и аморфных сплавов и твердых растворов. Плавление металлических стекол.   

Важные даты

прием докладов и регистрационных форм – до 1июня 2009

E-mail:  org.mcmo@gmail.com

Web: http://www.ip.rsu.ru/

II Междисциплинарный, международный симпозиум “Среды со структурным и магнитным упорядочением” (MULTIFERROICS-2),
23-28 сентября 2009, Ростов-на-Дону, п. Лоо

Тематика

1.        Свойства и теория пространственно неоднородных и геликоидальных магнитоупорядоченных фаз.

2.        Статические и динамические характеристики веществ, претерпевающих фазовые переходы в магнито-и структуроупорядоченные состояния.

3.        Взаимодействие магнитной подсистемы и химического упорядочения в упорядочивающихся твердых растворах и сплавах.

4.        Медьсодержащие соединения, претерпевающие фазовые переходы в состояние с высокотемпературной сверхпроводимостью:
       конкуренция и сосуществование магнитоупорядоченных и сверхпроводящих фаз.

5.        Новый класс высокотемпературных сверхпроводников – допированные фтором соединения с общей формулой ROFeAs, ROFeP
      (R – редкоземельный элемент).

6.        Многокомпонентные окислы переходных металлов (манганаты, хромиты, ортофериты), аномальные магнитотранспортные характеристики.

7.        Магнитострикционные фазовые переходы, магнитокаллористический эффект и эффект памяти формы.

8.        Слоистые материалы и сверхрешетки с магнитоэлектрическим эффектом.

Важные даты

прием докладов и регистрационных форм – до 1июня 2009

E-mail:  org.multiferroics@gmail.com

Web: http://www.ip.rsu.ru/

 

_____________________________________________

Внимание!

С апреля 2006 г. ПерсТ выпускается только в электронном формате и представлен по адресу http://www.issp.ac.ru/journal/perst и http://perst.isssph.kiae.ru . Желающие получать выпуски ПерсТа по своему электронному адресу могут сообщить его в адрес редакции perst@issp.ras.ru

Ответственный редактор И.Чугуева  irina@issp.ras.ru  тел: (495) 930 33 89

Научные редакторы: К.Кугель kugel@orc.ru, Ю.Метлин

В подготовке выпуска принимали участие:  О.Алексеева, В.Вьюрков, М.Компан, М.Маслов, Л.Опенов, К.Попов, А.Пятаков, В.Шагинян

Компьютерный ввод, макет: И.Фурлетова