IV International Astronomy Olympiad, Problems to solve

Euro-Asian Astronomical Society

IV International Astronomy Olympiad
Crimean Laboratory of SAI MSU and Crimean Astrophysical Observatory,
s. Nauchnyj, September 25 - October 2, 1999.

Problems to solve

Theoretical round

Text of these problems is available also
in other languages.

To solve every problem you may use constants and well-known values you know by heart.

Group A (juniors, < 16 years old).

1. The apparent diameter of the Moon, as seen from the Earth, is 31'. What is the image diameter in the objective focal plane if its focal length is 254 cm and the objective diameter is 40 cm? Draw a figure (a few figures) to explain your calculations.

2. A photometer is mounted on a 125 cm (focal length) telescope. Can you observe a star with magnitude

5^m
10^m
15^m

in a cluster if a count from a star of a similar spectral type with magnitude 8^m gives 4000 counts/second? The level of white noise of the photometer (instrumental noise) is 500 counts/second; the upper limiting value for observations is 200000 counts/second. Explain your calculations.

Group B (seniors, > 16 years old).

1. One star peaks at 2000 A. Another peaks at 10000 A. Which one emits more radiation at 2000 A? Which one emits more radiation at 10000 A? What is the ratio of the total radiation emitted by the two stars? Consider the stars as black bodies.

2. Engineers from the Simferopol University describe a new method to utilize old military ships: to construct very small black holes from their material (patent yzarc-048UA7). Estimate the diameter of a black hole constructed using this patent from a ship with the mass of 5000 tn (1 tn = 1000 kg). What physical object has a size of the same order of magnitude? Describe propagation of visible light near this black hole.

Other problems (3-9) are for the both (A and B) groups:

Theoretical round

3. Where (on the Earth) and when is it possible to observe the sunrise with the longest duration? Estimate its duration.

4. Usually we consider that there are about 6000 stars in the whole sky which are visible by our eyes. Estimate, how many visible stars are circumpolar (which means that they never set):

if you are placed 1° from the North Pole.
if you are placed 1° from the Equator (to the North).

Note: formula for sphere's area calculation: S = 4pR².

5. An airship started from a cosmodrome located near the equator of the earth at the moment of a sunset. A pilot of the airship wants to continue to observe the sun on the horizon. What should the speed of moving of the airship be? Describe in detail the motion of the air ship.

6. Suppose that a total solar eclipse is observed from a place at the equator when the sun is in zenith. Also, suppose that the shadow of the moon moves along the equator. Calculate the speed of the shadow relative to the observer.

Practical round

7. Write the observational program for this night on a 40-cm telescope.
What stars would you observe this nigth? Write sequence of the observations.
Stars to observe:

		V (mag)	a	d (1950)
1	h Aql	3^m.5	19^h 49^m.9	0° 53¢
2	b Per	2.1	3 04.9	40 46
3	c Cyg	14.2	19 48.6	32 47
4	R Aqr	12.4	23 41.2	-15 34
5	a Ori	1.3	5 52.4	7 24
6	RW Vir	6.7	12 04.7	-6 29

Moon rise: 21:17:26, phase 0.77
Sideral time for 0^h s₀ = 0:31:04
You may use all observational time (since 20h till 5h 30 min).
Local time LT=UT+3
Coordinates of observatory l = 2^h16^m j = 44°43¢
Put your result into the table:

Star	Interval of observation

Stars that could not be included in the program:
Explanations and notes:

8. A ligth curve of eclipsing binary is shown in the figure. Estimate the ratio of R/r in assuming that the eclipse is central and the small component is fainter.

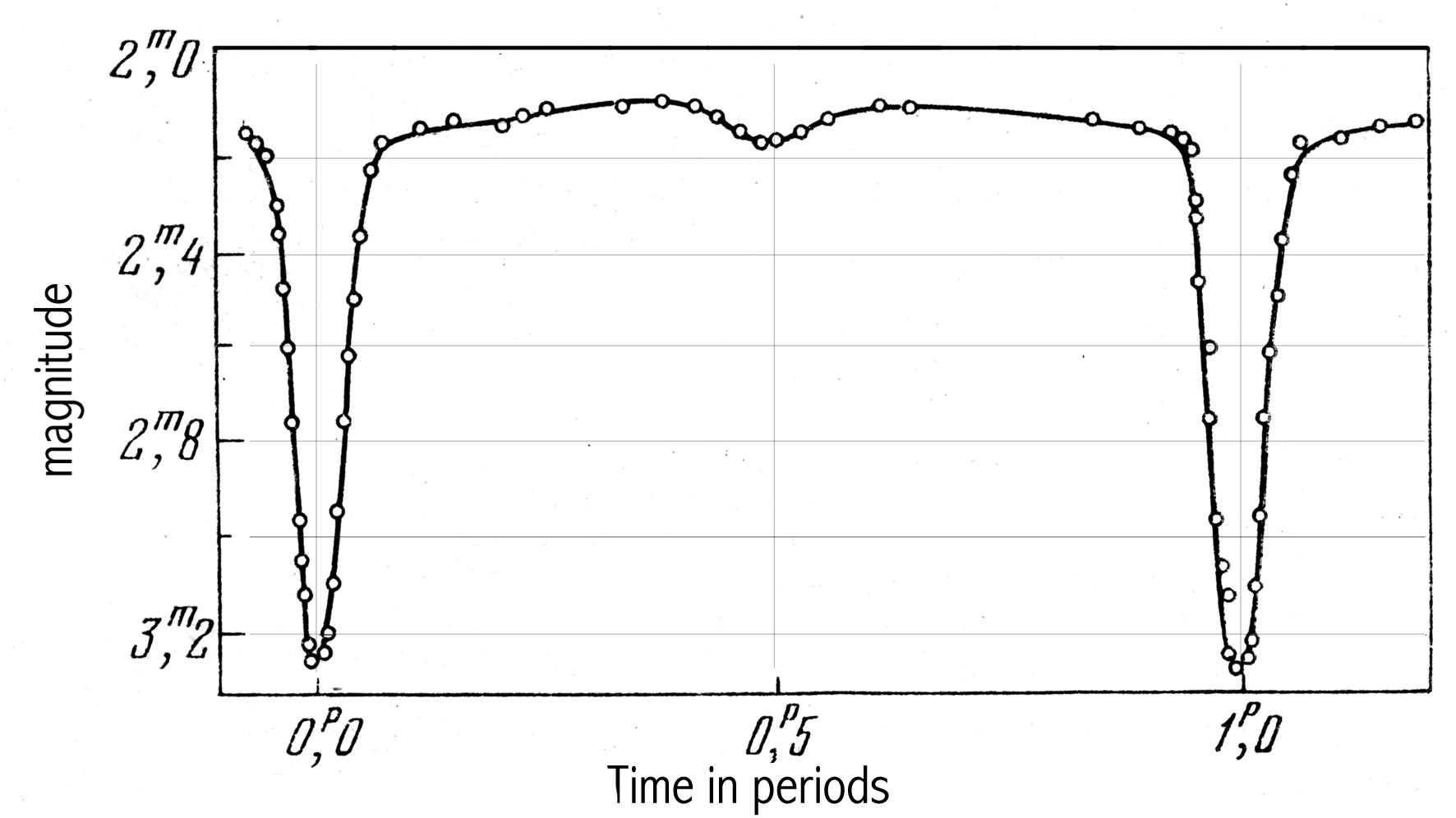
Observational round

9.1. Name the distance between the Moon and Jupiter in degree. Show how did you find the result.

9.2. Find and name the five brightesr stars of autumn sky. Which one is the brightest?

9.3. Define the period since new moon for today.

MGG * Naucnnyj * 1999 * Crimea