Введение

В.1 Общие замечания. Дифракционные методы в представлении обратной решетки.

Рентгеновский дифракционный анализ возник как результат принципиальных открытий 1912-1913 гг. Как пишет М.Лауэ - "Здесь оказались тесно связанными волновая теория рентгеновских лучей и атомистическая теория кристаллов - одно из тех поразительных событий, которые сообщают физике ее убедительную силу". За этим последовало внезапное взаимодействие таких весьма развитых, но разнородных областей, как физическая оптика и классическая кристаллография. Темп исследований был чрезвычайно высок: так, уже в первые десять лет - к 1922 г. были расшифрованы структуры более 40 чистых элементов и 100 неорганических фаз. Учтем при этом, что на стартовой позиции не были известны линейные масштабы - ни длины волн, ни параметры решеток. Именно в этот период были обеспечены структурные основы современной физики, химии и технологии конденсированных сред.

Для данного практикума полезно обратить внимание на своеобразную особенность рентгенографии, как экспериментального раздела - общепринятое "сосуществование" и взаимодействие рентгеновских методов разных уровней сложности в практике как исследовательских, так и промышленных лабораторий. Это означает, что "простейшие" схемы съемки, реализованные на начальных этапах - дебаевский, Лауэ, качания, гониометрия, - сохраняют необходимую роль в цепочке исследования и структурной аттестации наряду с автоматизированной техникой рентгеновской дифрактометрии. Соответственно, программа практикума предусматривает приобретение первоначальных навыков структурного анализа на базе рентгеновских дифракционных картин, полученных в различных схемах съемки.

При подготовке к выполнению работ полезно подчеркнуть специфику рентгеновского эксперимента в сравнении с дифракцией на линейной, либо двумерной решетке в оптическом диапазоне, известной со времен О.Френеля и Й.Фраунгофера. Рассеяние плоской (двумерной) волны на трехмерной трансляционной решетке создает новую ситуацию при наблюдении картины интерференции. В аналитической форме это проявляется в условиях Лауэ:

a(cos(α)-cos(α_o)) = λh
b(cos(β)-cos(β_o)) = λk
c(cos(γ)-cos(γ_o)) = λl
cos²(α)+cos²(β)+cos²(γ) = 1

Видно, что задача "переопределена": для трех неизвестных - направляющие косинусы дифрагированного луча - имеется система из четырех уравнений. В практическом плане это означает, что для получения дифракционной картины, кроме обычного соотношения между длиной волны и периодом решетки, требуется специальная конфигурация источник излучения - образец. Именно по этой причине возникает терминология - методы рентгеноструктурного анализа. Каждый из этих методов (или схем) отличается именно практическим способом преодоления указанного основного противоречия при дифракционных исследованиях кристаллической структуры. Соответственно, отдельный метод делает доступной лишь свою специфическую часть структурных характеристик; полная реализация возможностей рентгеновского эксперимента базируется на сочетании результатов, добытых в разных схемах съемки.

Трактовка методов структурного анализа делается наглядной при использовании общего подхода, связанного с понятием обратной решетки и построений Эвальда. Рассмотрим графический образ дифракционного эксперимента в метрике обратного пространства. В общепринятых обозначениях система координат обратной решетки задается:

a^* = [b×c]/(a[b×c]); b^* = [c×a]/(a[b×c]); c^* = [a×b]/(a[b×c]);

Соответственно, система плоскостей (hkl) отображается точкой с координатами G_hkl в обратном пространстве. Направление G_hkl в обратном пространстве параллельно нормали N_hkl к плоскости (hkl) в кристаллической решетке. Длина радиус-вектора для узла (hkl) вычисляется, как обратная величина межплоскостного расстояния G_hkl = 1/d. При этом вторые и все последующие порядки отражения от плоскости (hkl) располагаются в направлении радиус - вектора G_hkl на соответственно кратных расстояниях. В этой метрике весьма удобной оказывается векторная форма уравнения Вульфа - Брэгга. Если принимается для волновых векторов падающего и рассеянного монохроматического излучения k_o = k = 1/λ, то условия дифракции записываются, как:

k-k_o = G_hkl

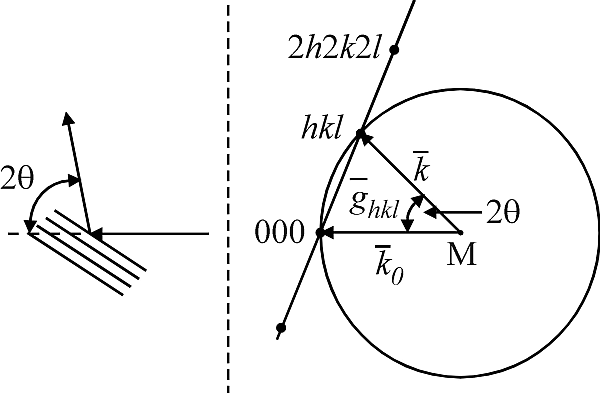
Рис. В.1.1 Построение Эвальда.

На рис В.1.1 представлен соответствующий векторный треугольник, впервые рассмотренный П. Эвальдом. Волновой вектор падающего излучения k_o оканчивается в начале координат обратной решетки; угол между падающим и дифрагированным лучом обозначается, как 2Θ. Видно, что тригонометрическое решение векторного треугольника M, (000), (hkl) совпадает с уравнением дифракции в форме 2sin(Θ)/λ = 1/d, аналогичной известному 2dsin(Θ) = λ. Наглядно видно, что в масштабе рисунка любой узел обратной решетки, попадающий на окружность (на сферу отражения, "сферу Эвальда") может дать дифракционный максимум. Однако, верно и негативное утверждение: при произвольной монохроматической длине волны и произвольном угле падения на кристалл возможны лишь случайные эпизоды возникновения отдельных дифракционных максимумов.

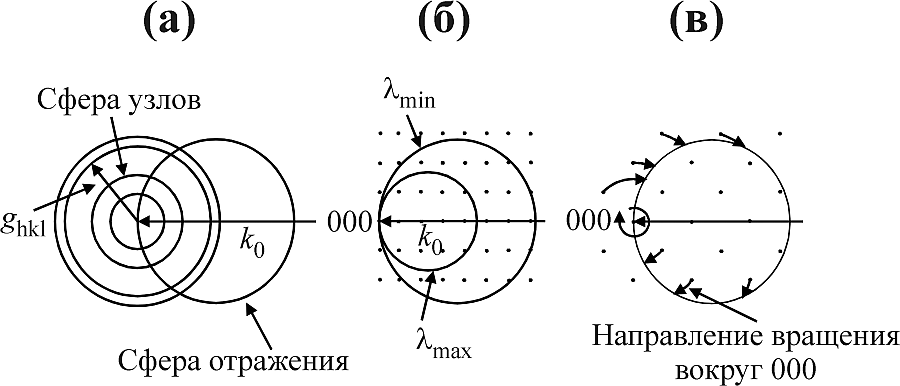
Рис. В.1.2 Графическая трактовка рентгеновской съемки.

Выбор экспериментального способа, обеспечивающего получение достаточно полной и информативной дифракционной картины от кристаллического материала и определяет различные схемы рентгеновской съемки. Рассмотрим графическую трактовку в обратном пространстве.

Дебаеграмма.

Объект - поликристаллический шлиф или порошок, излучение - монохроматическое.
В область первичного пучка попадает весьма большое количество беспорядочно ориентированных кристалликов, В обратном пространстве этому сопоставляются узлы обратной решетки hkl, которые воспроизводятся многократно на поверхности сферы с центром в <000>, имеющей радиус G_hkl = 1/d. Таким образом, в совокупном обратном пространстве поликристалла изображается система концентрических сфер, каждая из которых отвечает определенному межплоскостному расстоянию. Этим создаются условия, когда пересечение со сферой отражения определяет возникновение дебаевских конусов дифракции (рис В.1.2а).

Лауэграмма.

Объект - монокристалл, излучение - полихроматическое (тормозной спектр).
Распределение длин волн спектра падающего пучка отображается, как область непрерывного набора сфер отражения. Каждый узел обратной решетки попавший в эту область "выбирает себе" подходящую длину волны, соответствующую условиям дифракционного максимума (рис В.1.2б).

Рентгенограмма вращения (качания).

Объект - монокристалл, излучение - монохроматическое, движение - вращение образца во время съемки.
На (рис В.1.2в) показано, что дифракционные максимумы возникают не одновременно: они "вспыхивают" в ходе вращения кристалла по мере попадания отдельных узлов обратной решетки на сферу Эвальда.