Важнейшие научные результаты, полученные в ИФТТ РАН в 2013 году
|
8. Актуальные проблемы физики конденсированных сред, в том числе квантовой макрофизики, мезоскопики, физики наноструктур, спинтроники, сверхпроводимости |
|||||||||||||||||||
|
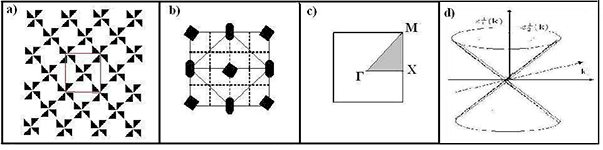
8-1. О новом типе безмассовых дираковских фермионов в кристаллических топологических изоляторах. Методы алгебраической топологии оказываются плодотворными во многих задачах от квантовой теории поля до физики конденсированного состояния. Хотя в своей основе математические методы являются общими, но в зависимости от постановки задачи они могут варьироваться. Кратко упомянем часто используемые подходы. Например, при классификации и выяснении устойчивости структурных дефектов, задача сводится к классификации классов эквивалентности гомотопических отображений некоторого стандартного многообразия, связанного с обхоом дефекта, в простанство параметра порядка. Классификация сводится к перечислению гомотопических групп, связанных с такими отображениями. В кристаллических изоляторах постановка задачи несколько отличается от упомянутых и сводится, в основном, к следующим вопросам.
2)Являются ли эти особенности устойчивыми при непрерывных деформациях гамильтониана системы, при которой сохраняется инвариантность гамильтонинана по отношению к пространственным элементам симметрии, инверсии времени, и которые не захлопывают щель в проекциях объемных зон, что приводит, к так называемой, Z2 классификации, отличной от упомянутой Z классификации кручений в импульсном пространстве. До сих пор, в кристаллических 3D→2D, в 2D→1D и чисто двумерных 2D системах, обсуждались особенности спектра с двукратным вырождением в симметричных точках ЗБ (конические ε ~ ±|k|, квадратичные ε ~ ±|k|2, кубические ε ~ ±|k|3). Конические особенности спектра обнаружены экспериментально в чисто 2D системах (графен), и в 3D→2D (двойные соединения BiSb и гетерограницы между полупроводниками А4В6 и А2В6 с инверсией зон) и 2D→1D кристаллических системах. Возникает вопрос о существовании конических особенностей в кристаллических системах с большей степенью вырождения. Вопрос о возможности появления и экспериментальном обнаружении таких особенностей (если таковые возможны) в кристаллических 3D→2D и чисто 2D системах является интересной и актуальной задачей. Поверхностные (краевые) состояния с коническим законом дисперсии и более чем с 2-х кратным вырождением 2D→1D системах отсутствуют, поскольку группы бордюров из-за «бедности» элементов симметрии не допускают более, чем 2-х кратное вырождение. Идеальной была бы ситуация, при которой можно было указать конкретные вещества или соединения, в которых возможна большая степень вырождения. Однако, на сегодняшний день это невозможно. Тем не менее, можно предъявить кристаллическую структуру, которую должно иметь соединение, чтобы в нем возникал конический безмассовый спектр с 4-х кратным вырождением. Именно эта задача решена в данной работе. Более того, оказывается, что в 3D→2D системах 4-х кратное вырождение конического спектра является максимально допустимым. (Лаборатория спектроскопии поверхности полупроводников, д.ф.-м.н., профессор С.Н.Молотков) |
|||||||||||||||||||
|
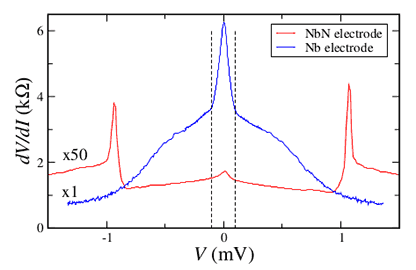
8-2. Подавление Андреевского отражения при энергиях много меньших чем сверхпроводящая щель. Появившийся в последнее время интерес к исследованию гибридных систем сверхпроводник – низкоразмерная электронная система был первоначально вызван проблемой поиска элементарных возбуждений типа Майорановского фермиона в твёрдом теле. Однако оказалось, что необходимый для реализации такого возбуждения режим топологической сверхпроводимости представляет самостоятельный интерес как с теоретической, так и с экспериментальной точек зрения. Режим топологической сверхпроводимости возникает в силу проникновения макроскопического параметра порядка через интерфейс между низкоразмерной электронной системой с сильным спин-орбитальным взаимодействием и сверхпроводником. Экспериментальные результаты в данной области пока достаточно противоречивы, в основном они были получены для случая одномерной системы – квантового провода. С другой стороны, хорошо известно, что край двумерной электронной системы проявляет чётко выраженные свойства одномерного транспорта как в квантующем, так и в нулевом магнитных полях. В этой связи можно поставить более общую экспериментальную задачу – исследование транспорта через интерфейс между двумерной электронной системой с сильным спин-орбитальным взаимодействием и металлом с макроскопическим параметром порядка. Исследован транспорт заряда через интерфейс между краем двумерной электронной системы в узкой квантовой яме InGaAs, характеризующейся сильным спин-орбитальным взаимодействием типа Рашбы, и металом с макроскопическим параметром порядка – сверхпроводником (Nb либо NbN).
Обнаружено (частичное) подавление Андреевского отражения на интерфейсе при сверхнизких температурах (менее 300 мК) и малых напряжениях смещения. Анализ магнетополевых и температурных зависимостей позволяет однозначно интерпретировать данное подавление как результат спин-орбитального взаимодействия в двумерной системе. Так же, в узкой области магнитных полей, соответствующих необходимым для реализации топологической сверхпроводимости, экспериментально обнаружен локальный пик в проводимости интерфейса при нулевых напряжениях смещения (zero bias anomaly). Частично (в части первых измерений ниобиевого контакта) эти результаты опубликованы в работе Письма в ЖЭТФ, 98, вып. 7, 477-483 (2013). |
|||||||||||||||||||
|
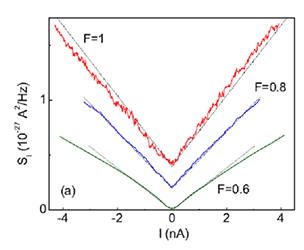
8-3. Размерный эффект в дробовом шуме при прыжковой проводимости В условиях термодинамического равновесия флуктуации электрического тока в проводнике определяются только его температурой и сопротивлением (тепловой шум Джонсона-Найквиста). При протекании электрического тока равновесие нарушается и возникают избыточные флуктуации, так называемый дробовой токовый шум. Такой шум является следствием дискретности элементарного заряда и достигает своего максимального значения при пуассоновской статистике протекания заряда. При низкой температуре кондактанс металлических и/или когерентных проводников определяется упругими процессами рассеяния. В таких системах дробовой шум наблюдается при условии, что размер исследуемого образца мал по сравнению с длиной энергетической релаксации на которой устанавливается локальное равновесие. Вопрос о наличии и величине дробового шума в диэлектрике с прыжковой проводимостью при конечной температуре не столь однозначен. Действительно, сам по себе прыжковый механизм проводимости существенно неупруг уже на масштабе одного прыжка (~ 100 нм), что, казалось бы, должно приводить к подавлению дробового шума в макроскопических образцах. В работе исследован дробовой шум в двумерной электронной системе в GaAs на образцах с длиной канала 5 мкм при температурах 0.5-4.2 К. Электронная плотность меняется при помощи фронтального металлического затвора. При низкой плотности достигается диэлектрическое состояние с температурной зависимостью проводимости, соответствующей моттовскому закону с переменой длиной прыжка. В этих условиях измеряется спектральная плотность токового шума на частотах выше 10 МГц, что на 2 порядка величины выше всех предыдущих исследований и позволяет надежно избежать влияния модуляционного/фликкер шума. При температуре 0.5К проводимость падает грубо экспоненциально с понижением электронной плотности, а величина дробового шума растет и достигает пуассоновского значения (фактор Фано сравнивается с 1 при сопротивлениях масштаба 10 МОм на квадрат). По-видимому, это первая демонстрация полного дробового шума в диэлектрике макроскопического размера. Также впервые продемонстрировано, что с повышением температуры дробовой шум заметно уменьшается (примерно втрое в исследованном интервале температур).
Эти результаты можно качественно объяснить, учитывая особенности протекания тока в прыжковом режиме. Как хорошо известно, бесконечный токонесущий кластер образуется на случайной сетке Миллера-Абрахамса с экспоненциально широким разбросом прыжковых сопротивлений. Корреляционная длина LC такого кластера значительно превышает среднюю длину прыжка и определяет характерный масштаб самоусреднения проводимости. При меньших LC размерах образца ток в нем протекает по квазиодномерным цепочкам, в каждой из которых преобладает одно самое большое прыжковое сопротивление. В результате полный токовый шум макроскопического образца определяется такими одиночными прыжками и достигает пуассоновского значения. Исходя из экспериментальных значений длины локализации и моттовской температуры, выход на пуассоновский шум наблюдается при значении LC ~ 1.5 мкм, что сравнимо с размером образца. Уменьшение LC при повышении температуры и/или увеличении длины локализации качественно объясняет наблюдаемое падение дробового шума. В то же время, падение дробового шума происходит медленнее, чем падает корреляционная длина, что может быть следствием плохой самоусредняемости. (Лаборатория квантового транспорта, к.ф.-м.н. В.С.Храпай) |
|||||||||||||||||||
|
8-4. Наблюдение нелокального сверхпроводящего тока в мезоскопической структуре с джозефсоновским переходом Разрабатываемые в настоящее время устройства сверхпроводящей наноэлектроники часто находятся в неравновесных условиях в связи с тем, что их размеры сравнимы с такими характерными длинами, как длина релаксации Эквивалентная “двух-жидкостная” схема, описывающая происходящие неравновесные процессы и соответствующая разработанной теоретической модели, показана в верхней части рисунка. Верхняя горизонтальная линия представляет сверхпроводящую компоненту, изменение электрохимического потенциала в ней происходит только в джозефсоновском переходе, отмеченном на рисунке крестиком. Изменение электрохимического потенциала нормальной компоненты (нижняя линия) происходит наоборот вдоль всей структуры. Наличие неравновесной разности потенциалов между линиями приводит к конверсии квазичастиц в куперовсие пары, которая определяется эффективной “поперечной проводимостью” G=(RlQ2)-1, где R-погонное нормальное сопротивление алюминиевой полоски. Рассмотрение в рамках предложенной модели показывает, что отношение Ic/Iinj,c соответствует доле инжектированных квазичастиц, которые достигают SNS перехода и компенсируются встречной сверхпроводящей компонентой, поскольку полный ток через переход в “нелокальном” эксперименте равен нулю. Обнаруженный эффект может быть полезен для подстраивания критических параметров джозефсоновских переходов неравновесными токами в схемах джозефсоновской электроники. (Лаборатория сверхпроводимости, д.ф.-м.н., проф. В.В.Рязанов) |
|||||||||||||||||||
|
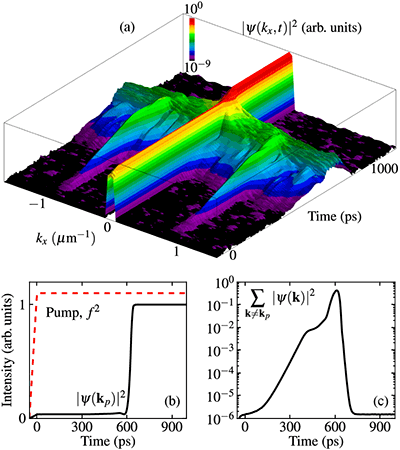
8-5. Режим с обострением в кинетике поляритонного конденсата В рамках теории на основе уравнения Гросса-Питаевского предсказано, что упругое параметрическое рассеяние может приводить к накоплению энергии поляритонного конденсата в условиях резонансной и когерентной оптической накачки. Состояние конденсата эволюционирует в режиме с обострением: медленное нарастание интенсивности, возникающее в точке порога рассеяния, за конечное время сменяется взрывообразным ростом и переходом на верхнюю ветвь устойчивости. Таким образом, открыт новый и существенно нелинейный механизм накопления энергии квантового резонатора с сильной экситон-фотонной связью. Этот механизм проявляется при фотовозбуждении со сравнительно большой отстройкой частоты накачки от поляритонного уровня. При этом амплитуда накачки слабо влияет на конечную амплитуду отклика резонатора, однако она определяет «время обострения», проходящее после «включения» накачки с данной амплитудой до начала быстрого усиления поля; это время может изменяться в очень широких пределах от нескольких времен жизни поляритона (при интенсивной накачке) до макроскопических величин (вблизи порога рассеяния). Приведенный рисунок иллюстрирует эффект «отложенного» во времени перехода между ветвями устойчивости бистабильного поляритонного конденсата. Микрорезонатор возбуждается в направлении нормали к поверхности на 0.5 мэВ выше поляритонного уровня при ширине резонанса 0.04 мэВ; время жизни поляритона составляет 16 пс. Мощность накачки на 10% превосходит порог рассеяния, но в 3 раза меньше, чем порог для перехода между ветвями устойчивости в одномодовой системе (без рассеяния). Сверху изображена интенсивность поля в резонаторе в зависимости от времени и планарной проекции волнового вектора (k = 0 соответствует возбуждаемой моде); внизу слева – интенсивности накачки (пунктирная линия) и возбуждаемой моды (сплошная линия), а справа – суммарная интенсивность рассеянных состояний в зависимости от времени. Видно, что медленное накопление энергии рассеянных мод, происходящее в течение 600 пс при строго постоянной внешней накачке, приводит в итоге к катастрофическому усилению поля в самой фотовозбуждаемой моде. Конечная интенсивность отклика лишь на 10% меньше той, которая могла бы быть достигнута без задержки во времени при накачке со втрое большей мощностью. 1. S. S Gavrilov, A. V. Sekretenko et al., Applied Physics Letters 102, 011104, 2013. |
|||||||||||||||||||
|
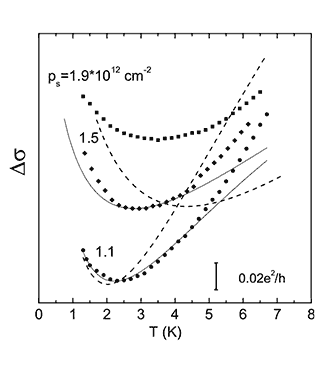
8-6. Влияние спин-орбитального взаимодействия на эффекты локализации электронов В температурной зависимости проводимости двумерных дырочных каналов кремниевых полевых транзисторов обнаружен кроссовер от слабой локализации при высоких температурах к антилокализации при низких. Наблюденный эффект удалось количественно описать, учитывая изменение соотношения между временами релаксации фазы электронной волны и спиновой релаксации, происходящее при изменении температуры. Проанализировано влияние на эффект квантовых поправок, обусловленных электрон - электронным взаимодействием. Анализ указывает на существование области параметров, в которой не происходит подавления электрон-электронным взаимодействием триплетного вклада в квантовую поправку к проводимости двумерной электронной системы со спин-орбитальным взаимодействием. (Сектор нанолитографии, д.ф.-м.н. С.И.Дорожкин) |
|||||||||||||||||||
|
9. Физическое материаловедение: новые материалы и структуры, в том числе фуллерены, нанотрубки, графены, другие наноматериалы, а также метаматериалы |
|||||||||||||||||||
|
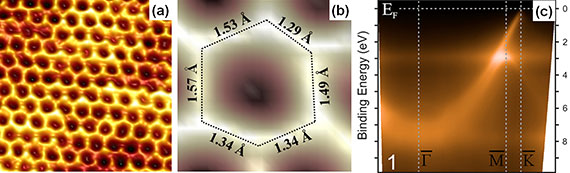
9-1. Синтез трехслойного графена однородной толщины Продемонстрирована возможность синтеза трехслойного графена однородной толщины на тонких пленках кубического карбида кремния SiC(001), выращенных на пластинах Si(001) миллиметрового размера. С помощью сканирующей туннельной микроскопии и электронной спектроскопии показано, что трехслойное графеновое покрытие на SiC(001) состоит из упорядоченной системы доменов, с границами раздела, ориентированными вдоль направлений [110] и [1-10]. Показано, что отдельные домены обладают свойствами и электронным спектром, характерными для монослойного графена. Ранее нами была показана возможность синтезировать на поверхности тонких (микронной толщины) монокристаллических пленок кубического карбида кремния, выращенных на стандартных пластинах Si(001) большого диаметра (> 300mm в диаметре). Такие пластины SiC(001)/Si(001) являются дешевыми и коммерчески доступными, поэтому синтез графена на них представляет собой существенный шаг на пути технологического применения этого материала и массового производства графена для электроники. В 2013 году детально исследована атомная и электронная структура графена, синтезированного на поверхности SiC(001). Полученные данные показали, что можно синтезировать непрерывное покрытие графена однородной толщины в диапазоне от 1 до 10 моноатомных слоев на поверхностях SiC (001) миллиметрового размера. Показано, что графеновое покрытие состоит из нескольких монослоев, обладающих атомной структурой (Рис. 1(а,b)) и электронным спектром (Рис. 1(с)) однослойного изолированного графена. ARPES исследования демонстрируют линейный спектр с точкой Дирака, близкой к уровню Ферми. В ходе исследований системы графен/SiC(001) показана возможность достижения пикометрового латерального разрешения (Рис. 1(b)), позволяющего визуализировать искажения решетки графена пикометрового масштаба в СТМ-экспериментах при комнатной температуре.
(Лаборатория спектроскопии поверхности полупроводников, д.ф.-м.н. В. Ю. Аристов, к. ф.-м.н. А. Н. Чайка, Nano Research 6 (2013) 562-570 |
|||||||||||||||||||
|
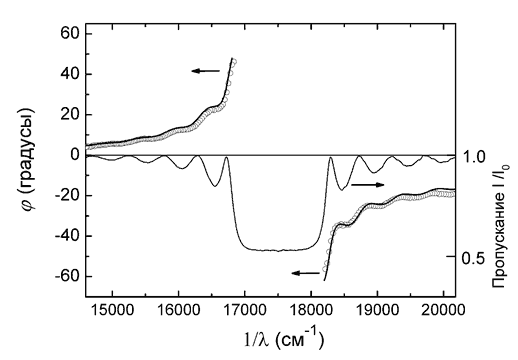
9-2. Жидкокристаллические фотонные кристаллы Приготовлены совершенные образцы жидкокристаллических фотонных кристаллов. В спектрах фазовой задержки (вращения плоскости поляризации света) обнаружены предсказанные теорией, но ранее не наблюдавшиеся особенности, связанные с маятниковыми колебаниями в спектрах дифракции. Показано, что оптические характеристики фотонных кристаллов, связанные с мнимой и действительной частью диэлектрической проницаемости, могут быть описаны на основе универсальных соотношений Крамерса-Кронига. Определены ширины фотонных запрещённых зон Δν, их температурная зависимость. Показано, что температурная зависимость относительной ширины фотонной запрещённой зоны Δν/ν0 может быть описана с использованием теории Ландау фазовых переходов первого рода.
Спектры пропускания и фазовой задержки (вращения плоскости поляризации света) холестерического фотонного кристалла. Экспериментальный и рассчитанный спектры φ показаны символами и сплошной кривой. (Лаборатория спектроскопии молекулярных структур, к.ф.-м.н. П.В.Долганов) |
|||||||||||||||||||
|
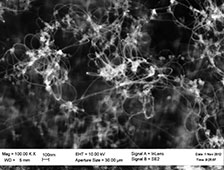
9-3. Массивы углеродных нанотрубок на металлических подложках Разработано устройство для получения массивов углеродных нанотрубок (УНТ) на металлических подложках (патент РФ на изобретение № 2471706, 2013) и предложены технологические методики получения слоев УНТ на подложках из нержавеющей стали, электротехнической стали и меди.
Полученные структуры применяются в качестве холодных катодов (ХК) в научной аппаратуре, используемой в исследованиях в области физики низких температур. Такие ХК сохраняют свою работоспособность вплоть до температур ≤ 4 К. В настоящее время данные холодные катоды не имеют аналогов. |
|||||||||||||||||||
|
9-4. Наноструктурированные и нанопористые углеродные материалы, полученные инвертированием глобулярных структур SiO2. Наноструктурные углеродные материалы привлекательны как с фундаментальной, так и с практической точки зрения и находят широкое применение во многих областях техники, включая электродные материалы для ионисторов, батарей и топливных элементов, сорбенты различного назначения, материалы для катализа. Наиболее активно развиваются направления, связанные с портативными источниками питания в микроэлектронике, накопителями энергии, компонентами силовых импульсных устройств и других приборов, где существует необходимость быстродействующего источника энергии. Важнейшими параметрами углеродных материалов, используемых в электрохимических источниках питания в качестве электродов, являются площадь удельной поверхности, размеры и топология пор. Высокая площадь удельной поверхности углерода повышает способность к аккумулированию зарядов на его поверхности. Основной вклад в площадь удельной поверхности вносят микропоры (диаметр менее 2 nm). Для быстрого переноса ионов в объеме электродного материала чрезвычайно важно присутствие мезопор (диаметр от 2 до 50 nm). Взаимосвязанная система микро - и мезопор в сочетании с высокой площадью поверхности электродов повышают выходные характеристики устройств. В ИФТТ РАН темплатным способом синтезированы микро- и мезопористые углеродные материалы со значениями площадей удельной поверхности, близкими к предельно возможной для углеродных материалов (2500 м2 /г), и объема пор до 2 см3/г. В качестве темплаты использована опаловая матрица, представляющая собой трёхмерную плотноупакованную систему монодисперсных шарообразных частиц (глобул) диоксида кремния. Взаимосвязанная система микро - и мезопор в инвертированном опале в сочетании с высокой площадью поверхности повышают как сорбционные, так и электрохимические выходные характеристики материала. На рис. 1 показана схема синтеза углеродных структур с решеткой инвертированного опала и фрагмент структуры, показывающий взаимосвязанную систему пор.
Показано, что наноструктуры обладают более богатым спектром свойств, в том числе и новыми функциональными свойствами, по сравнению с исследуемыми до сих пор материалами. Так, в структуре композитов обнаружены сферические частицы углерода, содержащие концентрические графитоподобные оболочки (onion-like), первые результаты исследований позволяют сделать предположение о наличии алмазоподобной фазы в композите SiC/C инвертированного опала. Углеродные наноструктуры с решеткой инвертированного опала (C-IOP), модифицированные тетрафенилметилендифосфин диоксидом, показали высокую сорбционную способность по отношению к ионам Th (IV), U (VI) и лантанидов (III) в растворах азотной кислоты в сравнении с известными сорбентами. В таблице 1 показаны коэффициент распределения Eu и фактор разделения La/Lu для нашего сорбента C-IOP и других углеродных сорбентов.
(Лаборатория кристаллизации из высокотемпературных растворов, |
|||||||||||||||||||
|
11. Фундаментальные основы лазерных технологий, включая обработку и модификацию материалов, оптическую информатику, связь, навигацию и медицину |
|||||||||||||||||||
|
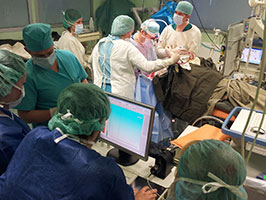
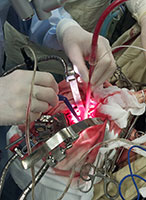
11-1. Сапфировый нейрохирургический скальпель В ИФТТ РАН разработан нейрохирургический сапфировый многоканальный зонд, открытые каналы зонда используются для аспирации, другие закрытые каналы содержат оптические волокна, по которым к рабочему концу инструмента передается коагулирующее лазерное излучение и диагностическое излучение. Диагностика с флуорофорами дает значительные преимущества при удалении опухолей мозга.
Излучение от источника лазерного излучения с помощью волокон доставляется к дистальному концу сапфирового зонда и, покидая зонд, поглощается в ткани, что приводит к ее коагуляции при достаточной мощности излучения. Длина волны излучения выбрана таким образом, чтобы не попадать в полосы поглощения диагностического флуоресцентного препарата для предотвращения его выгорания, а также, чтобы иметь оптимальную для нейрохирургии глубину проникновения и размер зоны лазерной коагуляции. Аспиратор с присоединенным к сапфировому зонду осуществляет удаление продуктов деструкции ткани мозга из зоны, диагностируемой как опухолевая ткань. Основные преимущества разработанного устройства: объединение в одном инструменте функций нескольких необходимых при проведении операции устройств; расширение функциональных возможностей нейрохирургического аспиратора введением дополнительной спектрометрической диагностикой ткани с применением флуорофоров, в том числе интерстициально, что позволяет объективно и оперативно выявлять наличие в ткани раковых клеток для оценки распространенности опухоли и правильности выбора объема резецируемой ткани; радикальность удаления внутримозговых опухолей, уменьшение травматичности операции и кровопотери, сокращение времени оперативного вмешательства за счет одновременного выполнения удаления, демаркации опухоли и остановки кровотечения. Сапфировый нейрохирургический зонд и способ удаления внутримозговых опухолей с его использованием разработаны совместно с сотрудниками нейрохирургического отделения МОНИКИ им. М.Ф. Владимирского. На способ и устройство получен Патент РФ. (Лаборатория профилированных кристаллов, д.т.н. В.Н.Курлов) |
|||||||||||||||||||






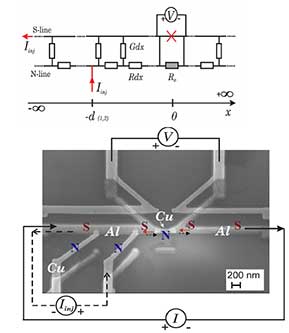 неравновесных нормальных носителей в куперовские пары lQ, длина спиновой диффузии lS и др. Возникновение обсуждаемого здесь эффекта обусловлено тем, что субмикронный планарный джозефсоновский переход (SNS мостик, находящийся в центре рисунка) был изготовлен вблизи инжектора неравновесных нормальных носителей (квазичастиц), так что расстояние d между инжектором (N) и SNS переходом было заметно меньше lQ, но существенно превышало сверхпроводящую длину когерентности xs. При инжектировании квазичастиц в ближайший сверхпроводящий алюминиевый берег SNS перехода “мимо” самого перехода (“нелокальный” завод тока показан пунктиром на рисунке) на переходе обнаруживалось напряжение при превышении током инжекции критического значения Iinj,c. Значение Iinj,c было значительно выше обычного критического тока Ic, измеряемого при “локальном” заводе тока в SNS переход (показан сплошной линией на рисунке).
неравновесных нормальных носителей в куперовские пары lQ, длина спиновой диффузии lS и др. Возникновение обсуждаемого здесь эффекта обусловлено тем, что субмикронный планарный джозефсоновский переход (SNS мостик, находящийся в центре рисунка) был изготовлен вблизи инжектора неравновесных нормальных носителей (квазичастиц), так что расстояние d между инжектором (N) и SNS переходом было заметно меньше lQ, но существенно превышало сверхпроводящую длину когерентности xs. При инжектировании квазичастиц в ближайший сверхпроводящий алюминиевый берег SNS перехода “мимо” самого перехода (“нелокальный” завод тока показан пунктиром на рисунке) на переходе обнаруживалось напряжение при превышении током инжекции критического значения Iinj,c. Значение Iinj,c было значительно выше обычного критического тока Ic, измеряемого при “локальном” заводе тока в SNS переход (показан сплошной линией на рисунке).