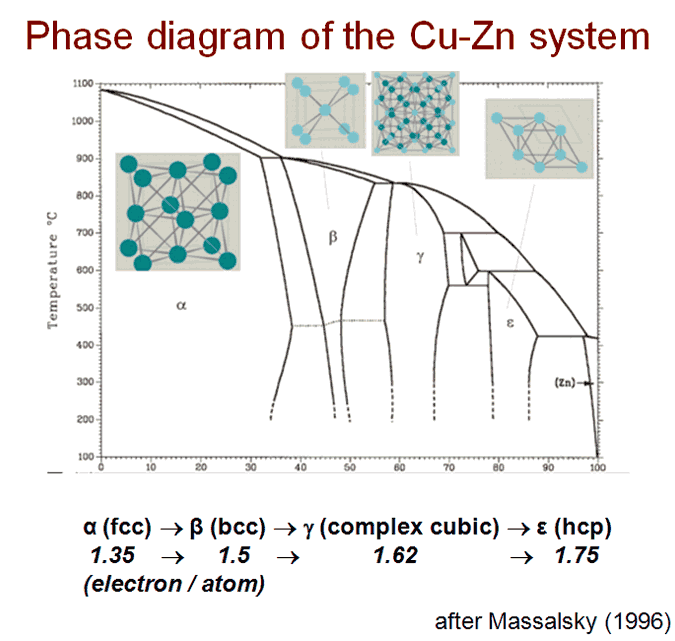
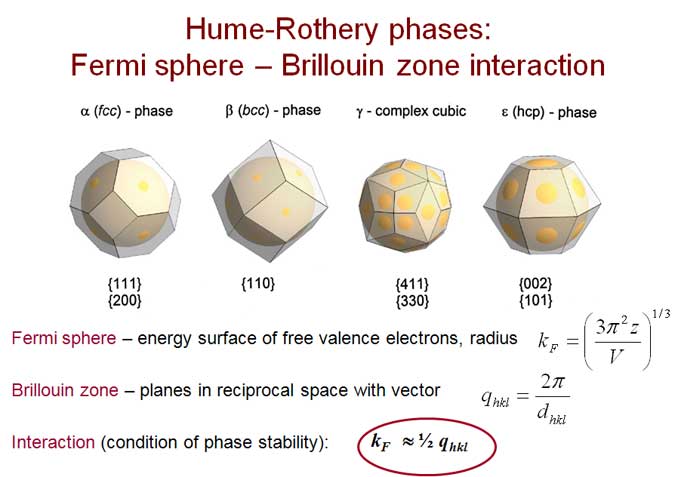
BRIZ: a vizualization program for Brillouin zone – Fermi sphere configuration

Introduction

The crystal structures of metals are usually characterized by high symmetry and by high coordination numbers. The most common examples are face-centered cubic (fcc), hexagonal close-packed (hcp) and body-centered cubic (bcc) structures. These structures are stabilized by the electrostatic or Ewald (E_Ew) energy that is the main part of the crystal energy. Another significant contribution to the crystal energy of metals is the electron-ion interaction or the electron bandstructure energy (E_BS) which is defined by the interaction of valence electrons and the Brillouin zone (BZ) planes. The existence of a BZ boundary close to the Fermi surface (FS) can open a pseudogap and reduce the overall electronic energy. FS-BZ interactions lead to formation of low-symmetry complex structures. This mechanism is used to account for stability of intermetallic phases usually called Hume-Rothery phases [1,2]. In the last decade, studies under high pressure on elemental metals have shown the transition to low-symmetry complex structures [3] demonstrating that E_BS contribution became important on compression.

The program BRIZ has been developed for 3D visualization of Brillouin zone configurations and intersections of BZ planes with a Fermi sphere[4]. The program can visualize the first Brillouin zone and larger Jones zones (both called for short as BZ) and can calculate the filling of the BZ by electron states. These estimations are important in the search for correlations between structures and physical properties, such as resistivity and superconductivity [5].

Theoretical background

Within the nearly-free-electron model valence electrons occupy the states in momentum space inside the Fermi spheres with the Fermi radius k_F =(3p² z/V)^1/3, where z is the number of valence electrons per atom and V is the atomic volume. In a metallic crystal electrons interact with a Brillouin plane corresponding to a reciprocal vector q_hkl if it is close to 2k_F . This condition, k_F ≈ ½q_hkl , leads to the opening of an energy gap and increasing in the density of electron states with reducing in the total electron energy. The energy gap is proportional to the square of the structure factor for a given plane. Thus, the E_BS contribution is important for those planes that give strong diffraction peaks and which are located with their wave vectors near position of 2k_F.

The classical example of phases stabilized by the E_BS term is the Cu-Zn alloy system. The constituent elements Cu and Zn are neighbors in the Periodic Table and therefore have minimal difference in atomic size and electronegativity. This implies that the main factor of the structure stabilization for intermediate phases is the electron concentration defined as an average number of valence electrons per atom [1,2]. The phase sequence in the Cu-Zn system is the following:

a (fcc) → b (bcc) → g (complex) → e (hcp).

The boundaries of phase regions are controlled by specific values of electron concentration:
1.35 → 1.5 → 1.62 → 1.75 (electrons/atom).

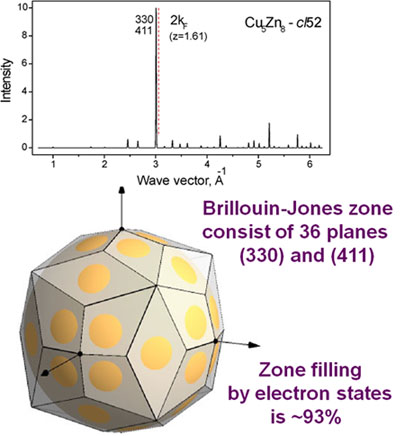
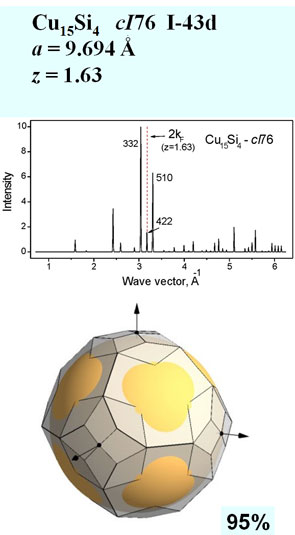
Similar phase sequences exist in many other binary systems containing a noble metal and a neighboring polyvalent element, called as Hume-Rothery phases. A complex gamma-brass phase of composition Cu₅ Zn₈ with 52 atoms in the unit cell (Pearson symbol cI52) is of special interest as an example when term E_BS is gaining over electrostatic term. This structure is a 3x3x3 supercell of bcc  with removing of 2 atoms from 54 and with slight rearrangement of the remaining 52 atoms to equalize interatomic distances. This gives an additional diffraction peak (411) with the same wave vector as for (330). The first explanation of the gamma-brass stability was done on the ground of a qualitative model of the Fermi sphere – Brillouin zone (FS-BZ) interaction [2]. The large Brillouin-Jones zone consists of 36 planes in close contact with the FS providing minimization of the crystal energy.

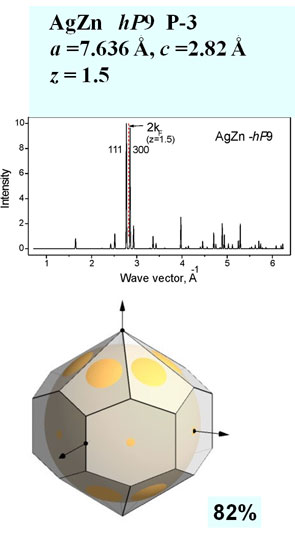
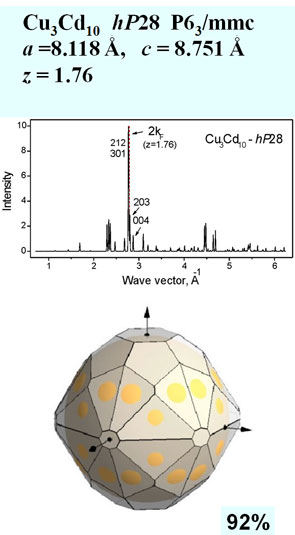
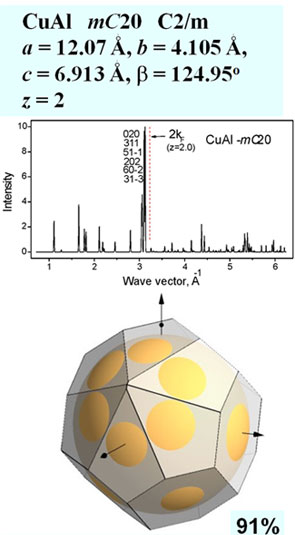
Capabilities

The program BRIZ is a 3D visualization system for the Brillouin zone configuration and a free-electron Fermi sphere with application of the graphical package OpenGL. BRIZ is written in Pascal and run on Windows XP. The program BRIZ can visualize the first Brillouin zone and large Brillouin-Jones zones. The intersections of zone planes with a Fermi sphere can be constructed and the volume of zones and Fermi spheres can be calculated. Estimation of zone filling by electron states is important for understanding of electronic properties and stability of a given phase.

Input data are the following: lattice parameters (a, b, c, a, b, g), number of atoms in the unit cell, number of valence electron per atom, list of hkl indices. The simplest way to select the necessary hkl indices is to estimate the value k_F and find the position of 2k_F on a diffraction pattern for a given phase and choose diffraction peaks with the nearest wave vector having strong structure factor. The program constructs BZ planes with selected hkl indices and the corresponding FS allowing rotation and showing different projections. Output data are volumes of BZ and FS, Fermi sphere radius and distances ½ q_hkl.

Examples

We consider some representative examples of the Hume-Rothery phases in binary sp-metal alloy system. Structural data are taken from Ref. [6].

Zone filling by electron states: volume (FS) / volume (BZ)

CuAl – mC20

(click on the image to see animation)

References

[1] Hume-Rothery, W.: Researches on the nature, properties, and condition of formation of intermetallic compounds, J. Inst. Metals359 (1926) 319-335.
[2] Mott, N.F. and Jones, H.: The Theory of the Properties of Metals and Alloys. Oxford University Press, London 1936.
[3] McMahon M.I., Nelmes R.J.: High-pressure structures and phase transformations in elemental metals. Chem. Soc. Rev. 35 (2006) 943-963.
[4] Degtyareva V.F., Smirnova I.S.: BRIZ: a vizualization program for Brillouin zone – Fermi sphere configuration, Z. Kristallogr. 222 (2007)718-721.
[5] Degtyareva , V.F.: Simple metals at high pressures: the Fermi sphere - Brillouin zone interaction model. Physics-Uspekhi 49 (2006) 369-388.
[6] Pearson, W.B.: A Handbook of Lattice Spacings and Structures of Metals. Pergamon Press, New York 1967.